题目内容
14.轮船在河流中来往航行于A、B两码头之间,顺流航行全程需7小时,逆流航行全程需9小时,已知水流速度为每小时3km,求A、B两码头间的距离.若设A、B两码头间距离为x,则所列方程为( )| A. | $\frac{x}{7}$+3=$\frac{x}{9}$-3 | B. | $\frac{x}{7}$-3=$\frac{x}{9}$+3 | C. | $\frac{x}{7}$+3=$\frac{x}{9}$ | D. | $\frac{x}{7}$-3=$\frac{x}{9}$ |
分析 首先理解题意找出题中存在的等量关系,再列出方程即可.
解答 解:设A、B两码头间距离为x,可得:$\frac{x}{7}-3=\frac{x}{9}+3$,
故选B
点评 此题考查一元一次方程的应用,列方程解应用题的关键是找出题目中的相等关系,注对于此类题目要意审题.

练习册系列答案
相关题目
5.某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为40%;
(2)甲班比赛成绩的方差S甲2=$\frac{26}{5}$,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
| 乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
(1)甲班的优秀率为60%,则乙班的优秀率为40%;
(2)甲班比赛成绩的方差S甲2=$\frac{26}{5}$,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
2.已知一个等腰三角形的一个内角是50°,则这个等腰三角形的另外两个内角度数分别是( )
| A. | 50°,80° | B. | 65°,65° | ||
| C. | 50°,80°或65°,65° | D. | 无法确定 |
9.下列线段能构成三角形的是( )
| A. | 2,7,4 | B. | 5,7,12 | C. | 7,15,10 | D. | 4,3,9 |
3.在平面直角坐标系中,把直线y=-2x+3沿y轴向上平移两个单位长度后,得到的直线的函数关系式为( )
| A. | y=-2x+1 | B. | y=-2x-5 | C. | y=-2x+5 | D. | y=-2x+7 |
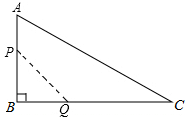 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)