题目内容
6.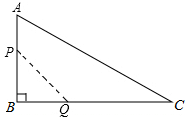 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
分析 由题意知BP=12-2t,BQ=4t,根据S=$\frac{1}{2}$BP×BQ可得答案.
解答 解:∵动点P从点A开始沿边AB向点B以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,
∴设t秒时,△PBQ的面积为S,根据题意得出:
S=$\frac{1}{2}$BP×BQ=$\frac{1}{2}$(12-2t)×4t=24t-4t2(0≤t≤6),
故答案为:S=24t-4t2(0≤t≤6).
点评 本题主要考查二次函数的应用,根据题意得出BP=12-2t,BQ=4t是结合三角形面积公式列出函数解析式的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.轮船在河流中来往航行于A、B两码头之间,顺流航行全程需7小时,逆流航行全程需9小时,已知水流速度为每小时3km,求A、B两码头间的距离.若设A、B两码头间距离为x,则所列方程为( )
| A. | $\frac{x}{7}$+3=$\frac{x}{9}$-3 | B. | $\frac{x}{7}$-3=$\frac{x}{9}$+3 | C. | $\frac{x}{7}$+3=$\frac{x}{9}$ | D. | $\frac{x}{7}$-3=$\frac{x}{9}$ |
1.抛物线y=2(x+3)2+5的顶点坐标是( )
| A. | (3,5) | B. | (-3,5) | C. | (3,-5) | D. | (-3,-5) |
18. 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )| A. | AD=$\frac{1}{2}$CD | B. | AC=$\frac{1}{2}$AB | C. | BD=$\frac{1}{2}$BC | D. | CD=$\frac{1}{2}$AB |

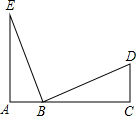 如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请依据ASA,添加一个适当的条件AE=EB,使得△EAB≌△BCD.
如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请依据ASA,添加一个适当的条件AE=EB,使得△EAB≌△BCD.