题目内容
16.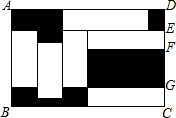 如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.
如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.
分析 设长方形的长和宽为未数,根据图示可得两个量关系:①小长方形的1个长+3个宽=16cm,②小长方形的1个长-1个宽=4cm,进而可得到关于x、y的两个方程,可求得解,从而可得到大长方形的面积,再根据阴影部分的面积=大长方形的面积-6个小长方形的面积求解即可.
解答 解:设小长方形的长为x,宽为y,如图可知,
$\left\{\begin{array}{l}{x+3y=16}\\{x-y=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$,
因此,大矩形ABCD的宽CD=4+3y=13(厘米).
阴影部分总面积=16×13-6×3×7=82(平方厘米),
故答案为:82.
点评 本题考查了二元一次方程的应用,以及学生对图表的阅读理解能力.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.

练习册系列答案
相关题目
6.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
| A. | 如果a∥b,a⊥c,那么b⊥c | B. | 如果b∥a,c∥a,那么b∥c | ||
| C. | 如果b⊥a,c⊥a,那么b⊥c | D. | 如果b⊥a,c⊥a,那么b∥c |
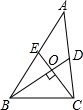 如图,已知BD,CE分别是△ABC的两条中线,BD⊥CE于点O,且CE=6,BD=8,则△ABC的面积为32.
如图,已知BD,CE分别是△ABC的两条中线,BD⊥CE于点O,且CE=6,BD=8,则△ABC的面积为32.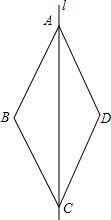 如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.
如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.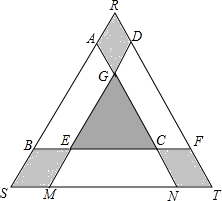 某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.
某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.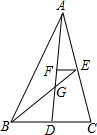 如图,线段AD、BE是△ABC的中线,AD、BE相交于点G,过点E作EF∥BC交AD于点F,若△ABC的面积为12,则△EFG的面积为$\frac{1}{2}$.
如图,线段AD、BE是△ABC的中线,AD、BE相交于点G,过点E作EF∥BC交AD于点F,若△ABC的面积为12,则△EFG的面积为$\frac{1}{2}$.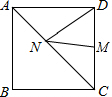 如图,在边长2正方形ABCD中,点M是CD的中点,在AC上确定点N,使DN+MN最小值是$\sqrt{5}$.
如图,在边长2正方形ABCD中,点M是CD的中点,在AC上确定点N,使DN+MN最小值是$\sqrt{5}$.