题目内容
4.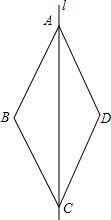 如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.
如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.
分析 根据轴对称图形的性质,四边形ABCD沿直线l对折能够完全重合,再根据两直线平行,内错角相等可得∠CAD=∠ACB=∠BAC=∠ACD,然后根据内错角相等,两直线平行即可判定AB∥CD,根据等角对等边可得AB=BC,然后判定出四边形ABCD是菱形,根据菱形的性质进行判断.
解答  解:∵l是四边形ABCD的对称轴,
解:∵l是四边形ABCD的对称轴,
∴∠CAD=∠BAC,∠ACD=∠ACB,
∵AD∥BC,
∴∠CAD=∠ACB,
∴∠CAD=∠ACB=∠BAC=∠ACD,
∴AB∥CD,AB=BC,故①②正确;
又∵l是四边形ABCD的对称轴,
∴AB=AD,BC=CD,
∴AB=BC=CD=AD,故④正确.
∴四边形ABCD是菱形,
∵菱形ABCD不一定是正方形,
∴AB⊥BC不成立,故③错误,
综上所述,正确的结论有①②④共3个.
故答案是:①②④.
点评 本题考查了轴对称的性质,平行线的性质,等角对等边的性质,熟记对称轴两边的部分能够完全重合是解题的关键.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为6,点E是BC的中点,点F在AB边上,BF=2AF,延长BC至点M,使得CM=AF.
如图,正方形ABCD的边长为6,点E是BC的中点,点F在AB边上,BF=2AF,延长BC至点M,使得CM=AF. 如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.
如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.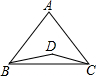 如图,已知AB=AC,BD=CD,∠BDC=150°,∠ABD=40°,求∠BAC的度数.
如图,已知AB=AC,BD=CD,∠BDC=150°,∠ABD=40°,求∠BAC的度数.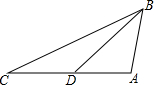 如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.
如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.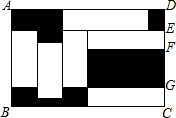 如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.
如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.