题目内容
5．
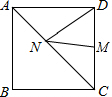如图，在边长2正方形ABCD中，点M是CD的中点，在AC上确定点N，使DN+MN最小值是$\sqrt{5}$．
分析 连接BM，甴正方形的性质可知点B、D关于直线AC对称，故BM即是DN+MN的最小值，根据勾股定理即可得出BM的长．
解答 
解：连接BM，
∵四边形ABCD是正方形，点M是CD的中点，
∴点B、D关于直线AC对称，CM=$\frac{1}{2}$CD=1，
∴BM即是DN+MN的最小值，
∴BM=$\sqrt{B{C}^{2}+C{M}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
练习册系列答案
相关题目
如图，正方形ABCD的边长为6，点E是BC的中点，点F在AB边上，BF=2AF，延长BC至点M，使得CM=AF．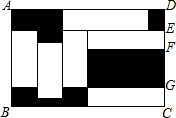
如图，在矩形ABCD中，放入六个形状，大小相同的长方形（即空白的长方形），AD=16cm，FG=4cm，则图中阴影部分的总面积是82 cm2．
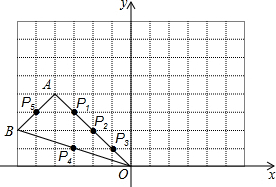如图，在边长为1的小正方形组成的网格中，△AOB的顶点都在格点上，点A、B的坐标分别为（-4，4）、（-6，2）．请按要求完成下列各题：
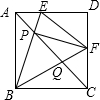如图，E是正方形ABCD中AD边上的一个动点，AC与BE交于点P，过P点作PF⊥BE交CD边于F点，连结EF、BF，若AB=4，下列结论