题目内容
1.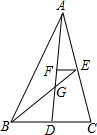 如图,线段AD、BE是△ABC的中线,AD、BE相交于点G,过点E作EF∥BC交AD于点F,若△ABC的面积为12,则△EFG的面积为$\frac{1}{2}$.
如图,线段AD、BE是△ABC的中线,AD、BE相交于点G,过点E作EF∥BC交AD于点F,若△ABC的面积为12,则△EFG的面积为$\frac{1}{2}$.
分析 由线段AD、BE是△ABC的中线得到S△ABD=$\frac{1}{2}$S△ABC=6,由于EF∥BC,推出△AEF∽△ACD,证得$\frac{EB}{BD}=\frac{1}{2}$,由△EFG∽△BDG,得到$\frac{DG}{DF}=\frac{2}{3}$,于是得到$\frac{DG}{AD}=\frac{1}{3}$,由于$\frac{{S}_{△EFG}}{{S}_{△BDG}}$=$\frac{1}{4}$,于是求得S△EFG=$\frac{1}{4}$S△BDG=$\frac{1}{2}$.
解答 解:∵线段AD、BE是△ABC的中线,
∴BD=CD,AE=CE,
∴S△ABD=$\frac{1}{2}$S△ABC=6,
∵EF∥BC,
∴△AEF∽△ACD,
∴$\frac{EF}{CD}=\frac{AE}{AC}=\frac{1}{2}$,
∴$\frac{EB}{BD}=\frac{1}{2}$,
∵EF∥BC,
∴△EFG∽△BDG,
∴$\frac{FG}{DG}=\frac{EF}{BD}=\frac{1}{2}$,
∴$\frac{DG}{DF}=\frac{2}{3}$,
∵DF=$\frac{1}{2}$AD,
∴$\frac{DG}{AD}=\frac{1}{3}$,
∴S△BDG=$\frac{1}{3}$S△ABD=2,
∵$\frac{{S}_{△EFG}}{{S}_{△BDG}}$=$\frac{1}{4}$,
∴S△EFG=$\frac{1}{4}$S△BDG=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了相似三角形的判定和性质,三角形面积,三角形中线,知道同高不同底的三角形的面积的比等于底的比是解题的关键.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | $\frac{a}{b}>\frac{a+c}{b+c}$ | B. | $\frac{a}{b}<\frac{a+c}{b+c}$ | C. | $\frac{a}{b}=\frac{a+c}{b+c}$ | D. | 前三种均有可能 |
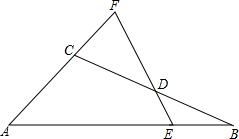 如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.
如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.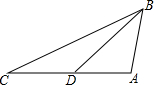 如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.
如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.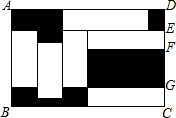 如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.
如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.