题目内容
7.已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D.(1)如图1,求证:BD=ED;
(2)如图2,AO为⊙O的半径,若BC=6,sin∠BAC=$\frac{3}{5}$,求OE的长.
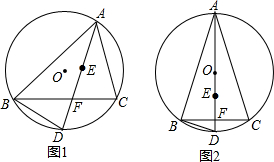
分析 (1)连接BE,由三角形的内心得出∠ABE=∠CBE,∠BAD=∠CAD,由圆周角定理得出∠DBC=∠CAD,得出∠DBC=∠BAD,再由三角形的外角性质得出∠DBE=∠DEB,即可得出结论.
(2)连接OB,由三角形的内心性质得出∠BAD=∠CAD,由圆周角定理得出$\widehat{BD}=\widehat{CD}$,由垂径定理得出BF=$\frac{1}{2}$BC=3,由圆周角定理得出∠BOD=2∠BAD=∠BAC,由三角函数得出OB=5,再由勾股定理求出OF,得出DF,再由勾股定理求出BD,得出ED,即可得出结果.
解答 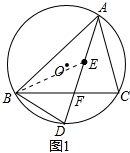 (1)证明:连接BE,如图1所示:
(1)证明:连接BE,如图1所示:
∵E是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD,
∵∠DBC=∠CAD,
∴∠DBC=∠BAD,
∵∠DBE=∠DBC+∠CBE,∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB,
∴BD=ED;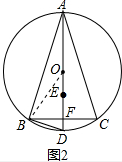
(2)解:连接OB,如图2所示:
∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴$\widehat{BD}=\widehat{CD}$,
∴BF=$\frac{1}{2}$BC=3,∠BOD=2∠BAD=∠BAC,
∵AE过点O,
∴AD⊥BC,
∴∠EFB=90°,
∴sin∠BAC=sin∠BOD=$\frac{BF}{OB}$=$\frac{3}{5}$,
∴OB=5,
∴OD=5,
∴OF=$\sqrt{O{B}^{2}-B{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴DF=OD-OF=1,
∴BD=$\sqrt{B{F}^{2}+D{F}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
由(1)得:ED=BD=$\sqrt{10}$,
∴OE=OD-ED=5-$\sqrt{10}$.
点评 本题考查了三角形的内心性质、圆周角定理、三角形的外角性质、等腰三角形的判定、勾股定理、垂径定理、三角函数等知识;本题有一定难度,特别是(2)中,需要运用垂径定理和两次运用勾股定理才能得出结果.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ab=1 | B. | a+b=0 | C. | a-b=0 | D. | a2=b2 |
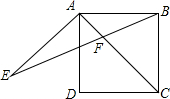 如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.
如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.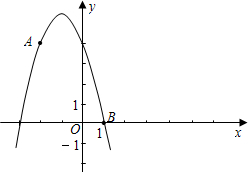 如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$
如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$