题目内容
17.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,则a与b的关系是( )| A. | ab=1 | B. | a+b=0 | C. | a-b=0 | D. | a2=b2 |
分析 先分母有理化求出a、b,再分别代入求出ab、a+b、a-b、a2、b2,求出每个式子的值,即可得出选项.
解答 解:a=$\frac{1}{2-\sqrt{3}}$=$\frac{1×(2+\sqrt{3})}{(2-\sqrt{3})×(2+\sqrt{3})}$=2+$\sqrt{3}$,
b=$\frac{1}{2+\sqrt{3}}$=$\frac{1×(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$,
A、ab=(2+$\sqrt{3}$)×(2-$\sqrt{3}$)=4-3=1,故本选项正确;
B、a+b=(2+$\sqrt{3}$)+(2-$\sqrt{3}$)=4,故本选项错误;
C、a-b=(2+$\sqrt{3}$)-(2-$\sqrt{3}$)=2$\sqrt{3}$,故本选项错误;
D、∵a2=(2+$\sqrt{3}$)2=4+4$\sqrt{3}$+3=7+4$\sqrt{3}$,b2=(2-$\sqrt{3}$)2=4-4$\sqrt{3}$+3=7-4$\sqrt{3}$,
∴a2≠b2,故本选项错误;
故选A.
点评 本题考查了分母有理化的应用,能求出每个式子的值是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.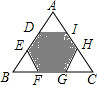 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
12. 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π+2\sqrt{3}$ | C. | 2$\sqrt{3}-\frac{5}{3}π$ | D. | $\sqrt{3}+\frac{5}{3}π$ |
 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=110°,则∠BCD的度数为125°.
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=110°,则∠BCD的度数为125°.