题目内容
2.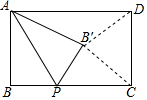 如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.
如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.
分析 如图,以CD为直径作⊙O,当点A到⊙O的最小距离等于AB时,使得△B′CD为直角三角形且唯一,在Rt△ADC中,根据AD2+OD2=OA2,可得b2+($\frac{1}{2}a$)2=(a+$\frac{1}{2}$a)2,即可推出b=$\sqrt{2}$a.
解答 解:如图, 以CD为直径作⊙O,当点A到⊙O的最小距离等于AB时,使得△B′CD为直角三角形且唯一,
以CD为直径作⊙O,当点A到⊙O的最小距离等于AB时,使得△B′CD为直角三角形且唯一,
在Rt△ADC中,∵AD2+OD2=OA2,
∴b2+($\frac{1}{2}a$)2=(a+$\frac{1}{2}$a)2,
整理得b2=2a2,
∵a>0,b>0,
∴b=$\sqrt{2}$a.
点评 本题考查翻折变换、矩形的性质、点与圆的位置关系、勾股定理等知识,解题的关键是学会利用辅助圆,寻找满足条件的图形,学会用方程的思想思考问题,属于中考填空题中的压轴题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
12.在实数-$\sqrt{2}$,-$\frac{1}{3}$,0,π,4中,无理数的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
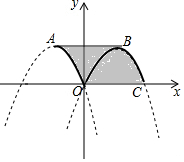 已知函数y=$\left\{\begin{array}{l}{-(x+1)^{2}+1(-1≤x<0)}\\{-(x-1)^{2}+1(0≤x≤2)}\end{array}\right.$,其图象如图中的实线部分,图象上两个最高点分别是A,B,连接AB,则图中曲四边形ABCO(阴影部分)的面积是2.
已知函数y=$\left\{\begin{array}{l}{-(x+1)^{2}+1(-1≤x<0)}\\{-(x-1)^{2}+1(0≤x≤2)}\end{array}\right.$,其图象如图中的实线部分,图象上两个最高点分别是A,B,连接AB,则图中曲四边形ABCO(阴影部分)的面积是2.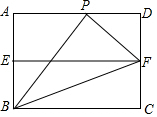 如图,在矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点,P是AD上一点,∠PFB=3∠FBC,则线段PD的长度$\frac{4}{3}$.
如图,在矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点,P是AD上一点,∠PFB=3∠FBC,则线段PD的长度$\frac{4}{3}$.