题目内容
10．一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对的概率小于$\frac{1}{1111}$，则密码的位数至少需要4位．分析 分别求出取一位数、两位数、三位数、四位数时一次就拨对密码的概率，再根据$\frac{1}{1111}$所在的范围解答即可．
解答 解：解：因为取一位数时一次就拨对密码的概率为$\frac{1}{10}$；
取两位数时一次就拨对密码的概率为$\frac{1}{100}$；
取三位数时一次就拨对密码的概率为$\frac{1}{1000}$；
取四位数时一次就拨对密码的概率为$\frac{1}{10000}$．
故一次就拨对的概率小于$\frac{1}{1111}$，密码的位数至少需要4位．
故答案为：4．
点评 本题考查了概率的求法与运用，一般方法为：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
1．-$\frac{3}{4}$的相反数是（ ）
| A． | $-\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $-|{\frac{3}{4}}|$ |
在如图所示的正方形网格中，每个小正方形的边长皆为1．请在网格上画出长度分别为$\sqrt{2}$，$\sqrt{5}$，$\sqrt{17}$的线段．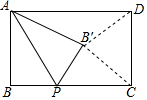
如图，在矩形ABCD中，AB=a，BC=b，点P是BC上的一个动点，连接AP，把△PAB沿着AP翻折到△PB′C（点B′在矩形的内部），连接B′C，B′D．点P在整个运动过程中，若存在唯一的位置使得△B′CD为直角三角形，则a，b之间的数量关系是b=$\sqrt{2}$a．
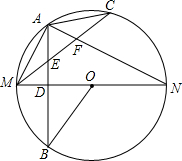如图所示，MN是⊙O的直径，作AB⊥MN，垂足为点D，连接AM，AN，点C为弧AN上一点，且$\widehat{AC}$=$\widehat{AM}$，连接CM，交AB于点E，交AN于点F，现给出以下结论：①MD=DO；②$\widehat{AM}$=$\widehat{BM}$；③∠ACM+∠ANM=∠MOB；④AE=$\frac{1}{2}$MF．其中正确的结论有②③④．（请把所有正确结论的序号都填在横线上）