题目内容
12.在实数-$\sqrt{2}$,-$\frac{1}{3}$,0,π,4中,无理数的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:无理数有-$\sqrt{2}$,π共2个.
故选C.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
4.任意抛掷一枚均匀的骰子,朝上点数为1的概率为$\frac{1}{6}$,有下列说法:①任意抛掷一枚均匀骰子12次,朝上点数为1的次数为2次;②任意抛掷一枚均匀骰子1200次,朝上点数为1的次数大约为200次,则你认为( )
| A. | ①②都对 | B. | ①②都错 | C. | ①对②错 | D. | ①错②对 |
1.-$\frac{3}{4}$的相反数是( )
| A. | $-\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-|{\frac{3}{4}}|$ |
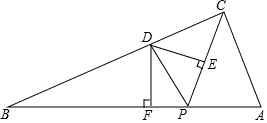 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$. 如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F
如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F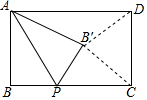 如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.
如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.