题目内容
11.如图1,在正方形ABCD中,点O是其几何中心(正方形的两条对角线的交点),∠MON=45°.(1)如图1,当点M在BC边上,ON与DC的延长线交于N点,写出BM,MN,CN之间的数量关系并证明你的结论;
(2)如图2,当点M在BC边上,ON与CD交于N点,写出BM,MN,CN之间的数量关系并证明你的结论;
(3)在(2)中,若正方形ABCD的边长为4,MC=1,求CN的长.
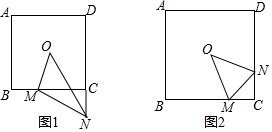
分析 (1)结论:MN=BM+CN.在CD上取一点G,使得CG=BM,只要证明△OBM≌△OCG,△ONM≌△ONG即可解决问题.
(2)结论:MN=BM-CN.在CD上取一点G,使得CG=BM,只要证明△OBM≌△OCG,△ONM≌△ONG即可解决问题.
(3)设CN=x,由CM=1,BC=4,推出BM=3.由BM=CN+MN,推出MN=3-x,在Rt△MNC中,根据MN2=CN2+CM2,列出方程即可解决问题.
解答 解:(1)结论:MN=BM+CN.
理由:在CD上取一点G,使得CG=BM.
在△OBM和△OCG中,
$\left\{\begin{array}{l}{OB=OC}\\{∠OBM=∠OCG}\\{BM=CG}\end{array}\right.$,
∴△OBM≌△OCG,
∴OM=OG,∠BOM=∠COG,
∵∠MON=45°,∠BOC=90°,
∴∠BOM+∠CON=∠CON+∠COG=45°,
∴∠NOM=∠NOG=45°,∵ON=ON,
∴△ONM≌△ONG,
∴NM=GN,
∵NG=CN+CG=CN+BM,
∴MN=BM+CN.
(2)结论:MN=BM-CN.
理由:在CD上取一点G,使得CG=BM.
在△OBM和△OCG中,
$\left\{\begin{array}{l}{OB=OC}\\{∠OBM=∠OCG}\\{BM=CG}\end{array}\right.$,
∴△OBM≌△OCG,
∴OM=OG,∠BOM=∠COG,
∴∠BOC=∠MOG=90°
∴∠NOM=45°,
∴∠NOG=45°
∴∠NOM=∠NOG,∵ON=ON,
∴△ONM≌△ONG,
∴NM=GN,
∵NG=CG-CN=BM-CN,
∴MN=BM-CN.
(3)设CN=x,
∵CM=1,BC=4,
∴BM=3.
∵BM=CN+MN,
∴MN=3-x,
在Rt△MNC中,∵MN2=CN2+CM2,
∴(3-x)2=x2+12,
∴x=$\frac{4}{3}$,
∴CN=$\frac{4}{3}$
点评 本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用方程的思想思考问题,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-|{\frac{3}{4}}|$ |
| A. | 361×106 | B. | 36.1×107 | C. | 3.61×108 | D. | 3.61×109 |
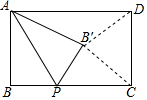 如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.
如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.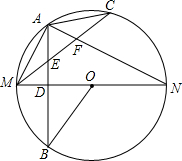 如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①MD=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正确的结论有②③④.(请把所有正确结论的序号都填在横线上)
如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①MD=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正确的结论有②③④.(请把所有正确结论的序号都填在横线上)