题目内容
17.某校八年级举行演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别为12元和8元.根据比赛设奖情况,需购买两种笔记本共30本,并且购买A笔记本的数量要少于B笔记本数量的$\frac{2}{3}$,但又不少于B笔记本数量的$\frac{1}{3}$.设买A种笔记本n本,买两种笔记本的总费用为W元.(1)请写出W(元)关于n(本)的函数关系式,并求出自变量n的取值范围.
(2)购买这两种笔记本各多少本时,花费最少?此时的花费是多少元?
分析 (1)根据题意可以求得w关于n的函数关系式,由购买A笔记本的数量要少于B笔记本数量的$\frac{2}{3}$,但又不少于B笔记本数量的$\frac{1}{3}$,可以确定n的取值范围;
(2)根据(1)中的函数关系式可以求得w的最小值及此时购买的A和B种两种笔记本的数量.
解答 解:(1)依题意得:w=12n+8(30-n)
即w=4n+240
且n<$\frac{2}{3}$(30-n)和n≥$\frac{1}{3}$(30-n)
解得$\frac{15}{2}$≤n<12
所以,w(元)关于n(本)的函数关系式为:w=4n+240
自变量n的取值范围是$\frac{15}{2}$≤n<12,n为整数;
(2)对于一次函数w=4n+240
∵w随n的增大而增大,且$\frac{15}{2}$≤n<12,n为整数
故当n为8时,w的值最小
此时,30-n=30-8=22,w=4×8+240=272(元)
因此,当买A种笔记本8本、B种笔记本22本时,所花费用最少,为272元.
点评 本题考查了一次函数的应用,一元一次不等式的应用.此题利用了(总花费=A种笔记本的单位价×A的数量+B种笔记本的单位价×B的数量),还用到了解不等式组以及一次函数的有关性质(当k>0时,y随x的增大而增大).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若a<b,则下列各式中一定正确的是( )
| A. | a-b>0 | B. | a+b>0 | C. | ab>0 | D. | -a>-b |
9.在Rt△ABC中,∠C=90°,AB=5,BC=3,则AC为( )
| A. | 4 | B. | 16 | C. | $\sqrt{34}$ | D. | 8 |
 如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F
如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F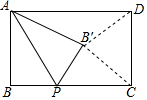 如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.
如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.