题目内容
1.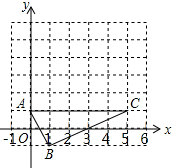 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)(1)判断△ABC的形状;
(2)将△ABC绕点C顺时针旋转90°得到△A1B1C,请在网格中画出△A1B1C,并直接写出点A1和B1的坐标;
(3)将△ABC绕线段AC所在直线旋转一周,求所得几何体的表面积.
分析 (1)根据勾股定理和勾股定理的逆定理即可判断△ABC的形状;
(2)根据图形旋转的性质画出图形,写出点A1和B1的坐标即可;
(3)所得几何体的表面积为底面半径为2,母线长为$\sqrt{5}$的圆锥侧面积与底面半径为2,母线长为2$\sqrt{5}$的圆锥侧面积的和.
解答 解:(1)∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AC=5,
($\sqrt{5}$)2+(2$\sqrt{5}$)2=52,
在△ABC中,AB2+BC2=AC2,
∴△ABC的形状是直角三角形;
(2)如图,△A1B1C即为所求.
由图可知,A1(5,6),B1(3,5);
(3)∵Rt△ABC中,∠ABC=90°,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AC=5,所得两个圆锥的底面半径都为2,
∴几何体的表面积=π×2×$\sqrt{5}$+π×2×2$\sqrt{5}$=6$\sqrt{5}$π.
故所得几何体的表面积为6$\sqrt{5}$π.
点评 本题考查的是作图-旋转变换,圆锥侧面积的计算,关键是熟知图形旋转不变性的性质,圆锥的侧面积=底面周长×母线长÷2的知识点.

练习册系列答案
相关题目
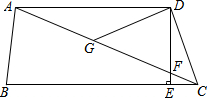 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为2$\sqrt{2}$.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为2$\sqrt{2}$.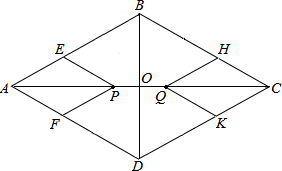 菱形ABCD的边长为2,∠BAD=60°,对角线AC,BD相交于点O,动点P在线段AC上从点A向点C运动,过P作PE∥AD,交AB于点E,过P作PF∥AB,交AD于点F,四边形QHCK与四边形PEAF关于直线BD对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,AP=x:
菱形ABCD的边长为2,∠BAD=60°,对角线AC,BD相交于点O,动点P在线段AC上从点A向点C运动,过P作PE∥AD,交AB于点E,过P作PF∥AB,交AD于点F,四边形QHCK与四边形PEAF关于直线BD对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,AP=x: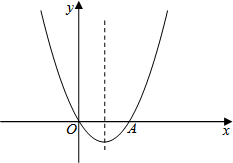 如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.
如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.