题目内容
13.解方程组$\left\{\begin{array}{l}{\frac{3x+2y}{4}=\frac{2x+y}{5}}\\{\frac{3x+2y}{4}=\frac{x-y+1}{6}}\\{\frac{2x+y}{5}=\frac{x-y+1}{6}}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{7x+6y=0①}\\{7x+8y=2②}\\{7x+11y=5③}\end{array}\right.$,
②-①得:2y=2,即y=1,
把y=1代入①得:x=-$\frac{6}{7}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{6}{7}}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列说法中错误的是( )
| A. | 一个锐角的补角一定是钝角 | |
| B. | 同角或等角的余角相等 | |
| C. | 两点间的距离是连结这两点的线段的长度 | |
| D. | 过直线l上的一点有且只有一条直线垂直于l |
5.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线平行,内错角相等 | |
| C. | 两直线被第三条直线所截,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
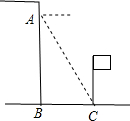 小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)
小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)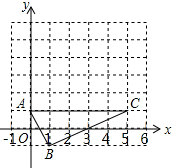 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)
 已知二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点.
已知二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点.