题目内容
10.已知实数x,y满足y=$\sqrt{x-1}$+$\sqrt{1-x}$-65,求$\root{3}{x-y}$.分析 根据二次根式有意义的条件,可得x、y的值,根据开立方,可得答案.
解答 解:∵实数x,y满足y=$\sqrt{x-1}$+$\sqrt{1-x}$-65,
∴$\sqrt{x-1}$=0且$\sqrt{1-x}$=0
∴x=1,y=-65
∴$\root{3}{x-y}$=$\root{3}{1-65}$=-4.
点评 本题考查了二次根式有意义的条件,利用二次根式的被开方数是非负数得出x、y的值是解题关键.

练习册系列答案
相关题目
20.下列计算不正确的一项是( )
| A. | $\frac{b}{2x}=\frac{by}{2xy}$ | B. | $\frac{ax}{bx}=\frac{a}{b}$ | ||
| C. | 3x2y÷$\frac{6{y}^{2}}{x}$=$\frac{{x}^{3}}{2y}$ | D. | $\frac{2a}{{a}^{2}-4}-\frac{1}{a-2}=\frac{1}{a+2}$ |
5.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线平行,内错角相等 | |
| C. | 两直线被第三条直线所截,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
15.下列五个代数式:①(x+y)(-x-y);②(2x-y)(y-2x);③(2a+3b)(3b-2a);④(2x-3y)(2y+3x);⑤(x+y+z)(z-x-y),能用平方差公式计算的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.已知△ABC的各边长度分别为3cm、4cm、5cm,则连接各边中点的三角形周长为( )
| A. | 2cm | B. | 7cm | C. | 5cm | D. | 6cm |
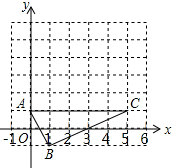 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1) 已知二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点.
已知二次函数y1=x2+bx+c的图象C1经过(-1,0),(0,-3)两点.