题目内容
12.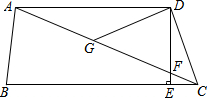 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为2$\sqrt{2}$.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为2$\sqrt{2}$.
分析 由AD与BC平行,且DE垂直于BC,得到DE垂直于AD,由G为AF的中点,即DG为斜边AF的中线,得到DG=AG=FG=3,利用等边对等角得到一对角相等,再由∠DGC为三角形ADG的外角,利用外角性质得到∠DGC=2∠GAD,再由两直线平行内错角相等得到∠GAD=∠ACB,设∠ACB=α,则有∠ACD=2α,进而得到∠DGC=∠DCG,利用等角对等边得到DG=DC,求出DC的长,在直角三角形DEC中,利用勾股定理求出DE的长即可.
解答 解:∵AD∥BC,DE⊥BC,
∴AD⊥DE,
∵G为AF的中点,即DG为斜边AF的中线,
∴DG=AG=FG=3,
∴∠GAD=∠GDA,
∵AD∥BC,
∴∠GAD=∠ACB,
设∠ACB=α,则∠ACD=2α,
∵∠GAD=∠GDA=α,
∴∠DGC=2α,即∠ACD=∠DGC,
∴DG=DC=3,
在Rt△DEC中,DC=3,EC=1,
根据勾股定理得:DE=$\sqrt{D{C}^{2}-E{C}^{2}}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$
点评 此题考查了勾股定理,等腰三角形的判定与性质,以及直角三角形斜边上的中线性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
20.下列计算不正确的一项是( )
| A. | $\frac{b}{2x}=\frac{by}{2xy}$ | B. | $\frac{ax}{bx}=\frac{a}{b}$ | ||
| C. | 3x2y÷$\frac{6{y}^{2}}{x}$=$\frac{{x}^{3}}{2y}$ | D. | $\frac{2a}{{a}^{2}-4}-\frac{1}{a-2}=\frac{1}{a+2}$ |
7.下列运算正确的是( )
| A. | 2x2÷x2=2x | B. | (-$\frac{1}{2}$a2b)3=-$\frac{1}{6}$a6b3 | C. | 3x2+2x2=5x2 | D. | (x-3)2=x2-9 |
17.下列运算中正确的是( )
| A. | a2•a3=a5 | B. | (a2)3=a5 | C. | a6÷a2=a3 | D. | a5+a5=2a10 |
4.下列说法中错误的是( )
| A. | 一个锐角的补角一定是钝角 | |
| B. | 同角或等角的余角相等 | |
| C. | 两点间的距离是连结这两点的线段的长度 | |
| D. | 过直线l上的一点有且只有一条直线垂直于l |
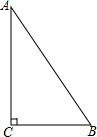 已知,如图所示,在Rt△ABC中,∠C=90°,
已知,如图所示,在Rt△ABC中,∠C=90°,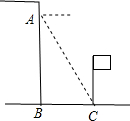 小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)
小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)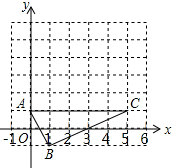 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1)