题目内容
11.已知线段AB=10cm,在直线AB上取一点C,使AC=16cm,则线段AB的中点与AC的中点的距离为( )| A. | 13cm | B. | 6cm | C. | 6cm或26cm | D. | 3cm或13cm |
分析 结合题意画出简单的图形,再结合图形进行分类讨论:当C在BA延长线上时,当C在AB延长线上时,分别依据线段的和差关系求解.
解答 解:①如图,当C在BA延长线上时,
∵AB=10cm,AC=16cm,D,E分别是AB,AC的中点,
∴AD=$\frac{1}{2}$AB=5cm,AE=$\frac{1}{2}$AC=8cm,
∴DE=AE+AD=8+5=13cm;
②如图,当C在AB延长线上时,
∵AB=10cm,AC=16cm,D,E分别是AB,AC的中点,
∴AD=$\frac{1}{2}$AB=5cm,AE=$\frac{1}{2}$AC=8cm,
∴DE=AE-AD=8-5=3cm;
故选D.
点评 本题主要考查了两点间的距离,解决问题的关键是依据题意画出图形,进行分类讨论.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | (ab)2=a2b2 | B. | 2(a+1)=2a+1 | C. | a2+a3=a6 | D. | a6÷a2=a3 |
20.计算:
(1)($\sqrt{3}$+$\sqrt{5}$)($\sqrt{3}$-$\sqrt{5}$)
(2)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$.
(1)($\sqrt{3}$+$\sqrt{5}$)($\sqrt{3}$-$\sqrt{5}$)
(2)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$.
1.不等式x<$\frac{2x+2}{3}$的正整数解的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
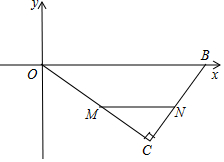 已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.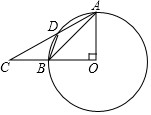 如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.
如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.