题目内容
13.若$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$是$\left\{\begin{array}{l}{αx+θy=1}\\{θx-βy=-2}\end{array}\right.$的解,则α、β之间的关系是( )| A. | β-9α=1 | B. | 9α+4β=1 | C. | 3α+2β=1 | D. | 4β-9α+1=0 |
分析 把$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$代入$\left\{\begin{array}{l}{αx+θy=1}\\{θx-βy=-2}\end{array}\right.$得关于θ、α、β的方程组,再利用加减消元法消去未知数θ即可.
解答 解:把$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$代入$\left\{\begin{array}{l}{αx+θy=1}\\{θx-βy=-2}\end{array}\right.$得:$\left\{\begin{array}{l}{-3α+2θ=1①}\\{-3θ-2β=-1②}\end{array}\right.$,
①×3+②×2得:-9α-4β=-1③,
③×(-1)得:9α+4β=1,
故选:B.
点评 此题主要考查了二元一次方程组的解,关键是掌握方程组的解同时满足两个方程.

练习册系列答案
相关题目
4.某班共有60人参加杜会实践拾棉花劳动,某天,这个班学生拾棉花的数量都在30kg以上,拾棉花的数量具体分组如表所示:
这天这个班学生平均没人拾棉花的数量约是41.3kg.(精确到0.1kg)
| 分组 | 31-35kg | 36-40kg | 41-45kg | 46-50kg | 51-55kg |
| 人数 | 8 | 23 | 15 | 9 | 5 |
1.不等式x<$\frac{2x+2}{3}$的正整数解的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
3.将分式方程$\frac{1}{x-3}$=$\frac{1}{x+3}$-$\frac{x+1}{{x}^{2}-9}$去分母,应在原方程两边同时乘的最简去分母为( )
| A. | (x+3)(x-3) | B. | x-3 | C. | x+3 | D. | x+1 |
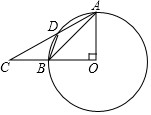 如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.
如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.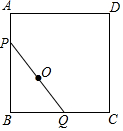 如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.
如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.