题目内容
7.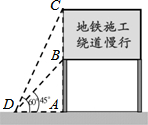 2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
分析 在Rt△ADB中,由∠BDA=45°,AB=3可得出DA=3,在Rt△ADC中,由特殊角的正切值即可得出线段CA的长度,再利用线段间的关系即可得出结论.
解答 解:∵在Rt△ADB中,∠BDA=45°,AB=3,
∴DA=3.
在Rt△ADC中,∠CDA=60°,
∴tan60°=$\frac{AC}{AD}$,
∴CA=DA•tan60°=3$\sqrt{3}$,
∴BC=CA-BA=3$\sqrt{3}$-3(米).
答:路况显示牌BC的高度是(3$\sqrt{3}$-3)米.
点评 本题考查了解直角三角形的应用中的俯角仰角问题,解题的关键是求出线段CA的长度.本题属于基础题,难度不大,解决该题型题目时,在直角三角形中结合特殊角的正切值找出线段间的关系是关键.

练习册系列答案
相关题目
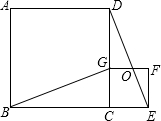 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{GO}{CE}$;④(a-b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{GO}{CE}$;④(a-b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )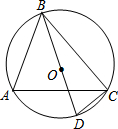 如图,⊙O的直径BD=4,∠A=60°,则BC的长度为2$\sqrt{3}$.
如图,⊙O的直径BD=4,∠A=60°,则BC的长度为2$\sqrt{3}$. 如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)
如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)