题目内容
2.山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.(1)今年A型车每辆售价多少元?(列方程解答)
(2)该车行计划今年新进一批A型车和B型车共60辆,A型车的进货价为每辆1100元,销售价与(1)相同;B型车的进货价为每辆1400元,销售价为每辆2000元,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
分析 (1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
解答 解:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由题意,得
$\frac{50000}{x+400}=\frac{50000(1-20%)}{x}$
解得:x=1600,
经检验,x=1600是元方程的根;
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由题意,得
y=(1600-1100)a+(2000-1400)(60-a),
y=-100a+36000,
∵B型车的进货数量不超过A型车数量的两倍,
∴60-a≤2a,
∴a≥20.
∵k=-100<0,
∴y随a的增大而减小.
∴a=20时,y最大=34000元.
∴B型车的数量为:60-20=40辆.
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,一次函数的解析式的运用,解答时由销售问题的数量关系求出一次函数的解析式是关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
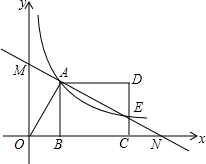 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.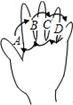 如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).
如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).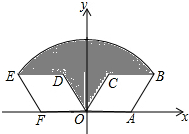 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.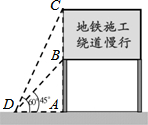 2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度. 函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )