题目内容
19. 如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)
如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)
分析 根据题意得出∠DAC=60°-30°=30°,进而得出AD=CD=40,再利用锐角三角函数关系求出AB即可.
解答 解:∵∠C=30°,∠ADB=60°,
∴∠DAC=30°,
∴AD=CD=40,
在Rt△ADB中,AB=AD×sin60°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$,
∴光岳楼AB的高度约为20$\sqrt{3}$m.
点评 此题主要考查了解直角三角形的应用,根据题意得出∠DAC=30°是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
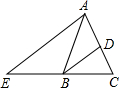 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).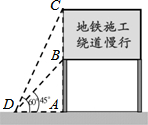 2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度. 函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( ) 如图,正方形ABCD的两边BC、AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3$\sqrt{2}$,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是$\frac{1}{3}$.
如图,正方形ABCD的两边BC、AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3$\sqrt{2}$,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是$\frac{1}{3}$.