题目内容
5.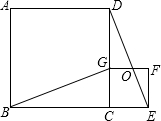 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{GO}{CE}$;④(a-b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{GO}{CE}$;④(a-b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由四边形ABCD和四边形CEFG是正方形,根据正方形的性质,即可得BC=DC,CG=CE,∠BCD=∠ECG=90°,则可根据SAS证得①△BCG≌△DCE;然后延长BG交DE于点H,根据全等三角形的对应角相等,求得∠CDE+∠DGH=90°,则可得②BH⊥DE;由△DGO与△DCE相似即可判定③错误,证明△EFO∽△DGO,即可求得④正确;即可得出结论.
解答 解:①∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,CD∥EF,
∴∠BCG=∠DCE.
在△BCG和△DCE中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCG=∠DCE}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
故①正确;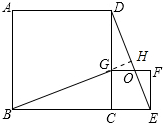
②延长BG交DE于点H,如图所示:
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE;
∴BG⊥DE.
故②正确;
③∵四边形GCEF是正方形,
∴GF∥CE,
∴$\frac{DG}{DC}=\frac{GO}{CE}$,
$\frac{DG}{GC}=\frac{GO}{CE}$是错误的.
故③错误;
④∵DC∥EF,
∴△EFO∽△DGO,
∴$\frac{{S}_{△EFO}}{{S}_{△DGO}}$=($\frac{EF}{DG}$)2=($\frac{b}{a-b}$)2=$\frac{{b}^{2}}{(a-b)^{2}}$,
∴(a-b)2•S△EFO=b2•S△DGO.
故④正确;
正确的有3个,故选:B.
点评 本题主要考查正方形的性质、全等三角形的判定和性质及相似三角形的判定和性质,综合性较强,掌握三角形全等、相似的判定和性质是解题的关键.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | a+2a=3a2 | B. | (a+b)2=a2+b2 | C. | (a2)3=a5 | D. | x7÷x5=x2 |
| A. | 2.5 | B. | 5 | C. | 2.5π | D. | 5π |
| A. | 9.8 | B. | 9.6 | C. | 9.5 | D. | 9.4 |
| A型汽车 | B型汽车 | |
| 满载量(吨) | 5 | 4 |
| 费用(元)/次 | 800 | 600 |
(1)求y与x之间的函数关系式;
(2)总租车费用最少是多少元?并说明此时的租车方案.
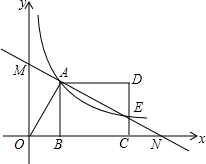 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
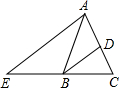 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).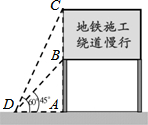 2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.