题目内容
如果多项式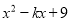 能用公式法分解因式,那么k的值是( )
能用公式法分解因式,那么k的值是( )
A. 3 B. 6 C. 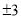 D.
D. 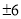
 D
【解析】由于可以利用公式法分解因式,所以它是一个完全平方式,所以.
故选:D.
D
【解析】由于可以利用公式法分解因式,所以它是一个完全平方式,所以.
故选:D.
练习册系列答案
相关题目
设a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,则a的最大值是( )
A. 480 B. 479 C. 448 D. 447
 D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D.
D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D. 下列哪个多项式能分解成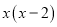 ( )
( )
A. 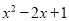 B.
B. 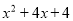 C.
C. 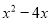 D.
D. 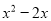
 D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D.
D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D. 若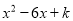 是一个完全平方式,那么k=_______________
是一个完全平方式,那么k=_______________
 9
【解析】因为若是一个完全平方式,那么,那么答案是k=9.
故答案为:9.
9
【解析】因为若是一个完全平方式,那么,那么答案是k=9.
故答案为:9. 分解因式: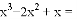 ______________.
______________.
 .
【解析】试题分析:==.故答案为:.
.
【解析】试题分析:==.故答案为:. 下列多项式能用完全平方公式分解因式的是( )
A. 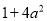 B.
B. 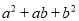 C.
C. 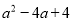 D.
D. 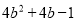
 C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C.
C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C. 如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
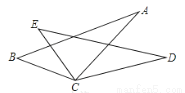
 AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
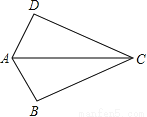
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
 C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC...
C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC... 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A. 7 B. 10 C. 35 D. 70
 C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C.
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C.