��Ŀ����
��֪����ABC������BD��CE���ڵ�O��F��G�ֱ���OB��OC���е㣮��֤���ı���DEFG��ƽ���ı��Σ�
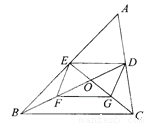
 ֤��������.
���������������������BD��CE�ǡ�ABC�����߿ɵ�DE�ǡ�ABC����λ�ߣ�F��G�ֱ���OB��OC���е�ɵ�FG�ǡ�BOC����λ�ߣ�������������λ�߶����ɵ�DE��BC��DE=BC��FG��BC��FG=BC�������ɵ�DE��FG��DE=FG������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵý���.
�����������BD��CE�ǡ�ABC�����ߣ���DE�ǡ�ABC����λ�ߣ�
��DE��B...
֤��������.
���������������������BD��CE�ǡ�ABC�����߿ɵ�DE�ǡ�ABC����λ�ߣ�F��G�ֱ���OB��OC���е�ɵ�FG�ǡ�BOC����λ�ߣ�������������λ�߶����ɵ�DE��BC��DE=BC��FG��BC��FG=BC�������ɵ�DE��FG��DE=FG������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵý���.
�����������BD��CE�ǡ�ABC�����ߣ���DE�ǡ�ABC����λ�ߣ�
��DE��B...
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д���ͼ����֪BC=EC����BCE=��ACD��Ҫʹ��ABC�ա�DEC����Ӧ���ӵ�һ������Ϊ ���𰸲�Ψһ��ֻ����һ����
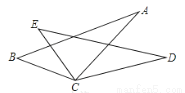
 AC=DC���B=��E���A=��D
�����������������������ݡ�BCE=��CAD�ɵá�BCA=��ECD������AC=DC��������SAS�������ж������ӡ�B=��E��������ASA�������ж������ӡ�A=��D��������AAS�������ж�.
AC=DC���B=��E���A=��D
�����������������������ݡ�BCE=��CAD�ɵá�BCA=��ECD������AC=DC��������SAS�������ж������ӡ�B=��E��������ASA�������ж������ӡ�A=��D��������AAS�������ж�. ���ݲ���ʽ�Ļ������ʣ������в���ʽ����x��a��x��a����ʽ��
(1)2x����4; (2)x��4����2��
(3)��2x��1; (4)  x��2.
x��2.
 (1)x����2 (2)x��2 (3)x���� (4)x��4
�����������������������ʽ���ò���ʽ�Ļ������ʱ��λ�Ϊx��a��x��a����ʽ���ɣ�
���������(1)2x����4��
����ͬʱ����2����
x>-2��
(2)x��4����2��
����ͬʱ����4����
x<2��
(3)��2x��1��
����ͬʱ����-2����
x���� ��
(4) x��2��
��...
(1)x����2 (2)x��2 (3)x���� (4)x��4
�����������������������ʽ���ò���ʽ�Ļ������ʱ��λ�Ϊx��a��x��a����ʽ���ɣ�
���������(1)2x����4��
����ͬʱ����2����
x>-2��
(2)x��4����2��
����ͬʱ����4����
x<2��
(3)��2x��1��
����ͬʱ����-2����
x���� ��
(4) x��2��
��... ��һ����n���ε�ÿ���ڽ�Ϊ144�㣬�������n���ε����жԽ��ߵ������ǣ�������
A. 7 B. 10 C. 35 D. 70
 C
������������n���ε�ÿ���ڽ�Ϊ144���϶�����ڽǺ�ʽ�����ɵó�����n��һԪһ�η��̣��ⷽ�̼������n��ֵ����������м��ɵó����ۣ�
��������
��һ����n���ε�ÿ���ڽ�Ϊ144�㣬
��144n=180����n��2������ã�n=10��
�����n���ε����жԽ��ߵ������ǣ�==35��
��ѡC��
C
������������n���ε�ÿ���ڽ�Ϊ144���϶�����ڽǺ�ʽ�����ɵó�����n��һԪһ�η��̣��ⷽ�̼������n��ֵ����������м��ɵó����ۣ�
��������
��һ����n���ε�ÿ���ڽ�Ϊ144�㣬
��144n=180����n��2������ã�n=10��
�����n���ε����жԽ��ߵ������ǣ�==35��
��ѡC�� ��ͼ�ڡ�ABC�У�D��E�ֱ�ΪAB��AC�ϵĵ㣬��BD��CE��M��N�ֱ���BE��CD���е㣮��MN��ֱ�߽�AB��P����AC��Q���߶�AP��AQ�����?Ϊʲô?
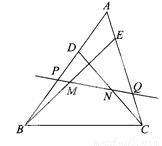
 AP=AQ�����ɼ�����.
��������������λ�߶���֤��MH=NH������֤����HMN=��HNM����HMN=��PQA�����ԡ�APQΪ���������Σ���AP=AQ��
AP=AQ�����ɼ�����.
��������������λ�߶���֤��MH=NH������֤����HMN=��HNM����HMN=��PQA�����ԡ�APQΪ���������Σ���AP=AQ�� ��ͼ�����ı���ABCD�У���ABC=90�㣬AC=AD��M��N�ֱ�ΪAC��CD���е㣬����BM��MN��BN��
��1����֤��BM=MN��
��2����BAD=60�㣬ACƽ�֡�BAD��AC=2����BN�ij���
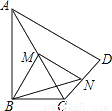
 ��1��֤������������2��
�������������������1���ڡ�CAD�У�����λ�߶����õ�MN��AD����MN=AD����Rt��ABC�У���ΪM��AC���е㣬��BM=AC�����ɵõ����ۣ�
��2���ɡ�BAD=60����ACƽ�֡�BAD���õ���BAC=��DAC=30�㣬�ɣ�1��֪��BM=AC=AM=MC���õ���BMC =60�㣮��ƽ�������ʵõ���NMC=��DAC=30�㣬�ʡ�BMN90�㣬�õ�������MN=...
��1��֤������������2��
�������������������1���ڡ�CAD�У�����λ�߶����õ�MN��AD����MN=AD����Rt��ABC�У���ΪM��AC���е㣬��BM=AC�����ɵõ����ۣ�
��2���ɡ�BAD=60����ACƽ�֡�BAD���õ���BAC=��DAC=30�㣬�ɣ�1��֪��BM=AC=AM=MC���õ���BMC =60�㣮��ƽ�������ʵõ���NMC=��DAC=30�㣬�ʡ�BMN90�㣬�õ�������MN=... ��ͼ�����ı���ABCD�У�P�ǶԽ���BD���е㣬E��F�ֱ���AB��CD���е㣬AD=BC����PEF=18�㣬���PFE�Ķ����� �ȣ�
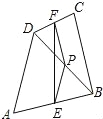
 18��
��������
���������������λ�߶�������֪����֤����EPF�ǵ��������Σ������ı���ABCD�У�P�ǶԽ���BD���е㣬E��F�ֱ���AB��CD���е㣬��FP��PE�ֱ��ǡ�CDB���DAB����λ�ߣ���PF=BC��PE=AD����AD=BC����PF=PE���ʡ�EPF�ǵ��������Σ��ߡ�PEF=18�㣬���PEF=��PFE=18�㣮�ʴ�Ϊ��18��
18��
��������
���������������λ�߶�������֪����֤����EPF�ǵ��������Σ������ı���ABCD�У�P�ǶԽ���BD���е㣬E��F�ֱ���AB��CD���е㣬��FP��PE�ֱ��ǡ�CDB���DAB����λ�ߣ���PF=BC��PE=AD����AD=BC����PF=PE���ʡ�EPF�ǵ��������Σ��ߡ�PEF=18�㣬���PEF=��PFE=18�㣮�ʴ�Ϊ��18�� һ����ѧ�����Ӱ������ܵļ�¼��11.7�룬����һ�����˶�Ա�İ������ܳɼ�Ϊx�룬��������˶�Ա�Ƽ�¼����__________����������˶�Աû�Ƽ�¼����________��
 x��11.7�� x��11.7
��������������ã��߰������ܵļ�¼��11.7�룬
��Ҫ�Ƽ�¼��x��ll��7��
û�Ƽ�¼x��11.7��
�ʴ�Ϊ��x��11.7��x��11.7��
x��11.7�� x��11.7
��������������ã��߰������ܵļ�¼��11.7�룬
��Ҫ�Ƽ�¼��x��ll��7��
û�Ƽ�¼x��11.7��
�ʴ�Ϊ��x��11.7��x��11.7�� ��֪��Rt��ABC��,б��AB=2BC,��ֱ��ACΪ�Գ���,��B�ĶԳƵ���B',��ͼ��ʾ,�����߶�BC��ȵ��߶���____�����߶�AB��ȵ��߶���_______��_______,���B��ȵĽ���________��_______,��˿ɵõ���B=________.

 B�� C AB�� BB �� ��B�� ��BAB�� 60��
������������ֱ��ACΪ�Գ���,��B�ĶԳƵ���B' ��
��B��C=BC �� ��B��CA=��BCA=90�㣬AB��=AB=2BC��
��AB��=AB=BB�䣬
���B��=��B=��B��AB =60��.
B�� C AB�� BB �� ��B�� ��BAB�� 60��
������������ֱ��ACΪ�Գ���,��B�ĶԳƵ���B' ��
��B��C=BC �� ��B��CA=��BCA=90�㣬AB��=AB=2BC��
��AB��=AB=BB�䣬
���B��=��B=��B��AB =60��. 
