题目内容
当x=_____时,分式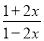 的值为零.
的值为零.
 【解析】由题意可得1+2x=0且1-2x≠0,解得x=.
故当x=时,分式的值为零。故答案为: .
【解析】由题意可得1+2x=0且1-2x≠0,解得x=.
故当x=时,分式的值为零。故答案为: .
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列哪个多项式能分解成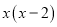 ( )
( )
A. 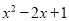 B.
B. 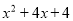 C.
C. 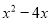 D.
D. 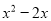
 D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D.
D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D. 如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
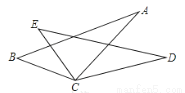
 AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
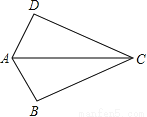
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
 C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC...
C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC... 不改变分式的值,使分式的分子、分母中的首项的系数都不含 “-” 号.
①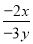 =___________; ②
=___________; ②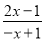 =__________________;
=__________________;
③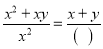 =_________;④
=_________;④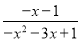 =______________.
=______________.
 【解析】①= ;
②=;
③=
④=.故答案为: (1). (2). (3). (4).
【解析】①= ;
②=;
③=
④=.故答案为: (1). (2). (3). (4). 化简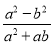 的结果为( )
的结果为( )
A. 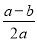 B.
B. 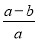 C.
C. 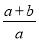 D.
D. 
 B
【解析】=,故选B.
B
【解析】=,故选B. 根据不等式的基本性质,把下列不等式化成x>a或x<a的形式:
(1)2x>-4; (2)x-4<-2;
(3)-2x<1; (4)  x<2.
x<2.
 (1)x>-2 (2)x<2 (3)x>- (4)x<4
【解析】试题分析:各不等式利用不等式的基本性质变形化为x>a或x<a的形式即可.
试题解析:(1)2x>-4,
两边同时除以2,得
x>-2;
(2)x-4<-2,
两边同时加上4,得
x<2;
(3)-2x<1,
两边同时除以-2,得
x>- ;
(4) x<2,
两...
(1)x>-2 (2)x<2 (3)x>- (4)x<4
【解析】试题分析:各不等式利用不等式的基本性质变形化为x>a或x<a的形式即可.
试题解析:(1)2x>-4,
两边同时除以2,得
x>-2;
(2)x-4<-2,
两边同时加上4,得
x<2;
(3)-2x<1,
两边同时除以-2,得
x>- ;
(4) x<2,
两... 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A. 7 B. 10 C. 35 D. 70
 C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C.
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C. 一所中学的男子百米赛跑的记录是11.7秒,假设一名男运动员的百米赛跑成绩为x秒,如果这名运动员破记录,则__________;如果这名运动员没破记录,则________.
 x<11.7, x≥11.7
【解析】由题意得:∵百米赛跑的记录是11.7秒,
∴要破纪录则x<ll.7,
没破纪录x≥11.7,
故答案为:x<11.7,x≥11.7.
x<11.7, x≥11.7
【解析】由题意得:∵百米赛跑的记录是11.7秒,
∴要破纪录则x<ll.7,
没破纪录x≥11.7,
故答案为:x<11.7,x≥11.7. 
