题目内容
3.已知:x=2-$\sqrt{2}$,求$\frac{{x}^{2}-4}{x}$•($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)÷$\frac{{x}^{2}-2x-8}{{x}^{2}}$的值.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{(x+2)(x-2)}{x}$•[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]•$\frac{{x}^{2}}{(x+2)(x-4)}$
=$\frac{(x+2)(x-2)}{x}$•$\frac{{x}^{2}-4-{x}^{2}+x}{{x(x-2)}^{2}}$•$\frac{{x}^{2}}{(x+2)(x-4)}$
=$\frac{(x+2)(x-2)}{x}$•$\frac{x-4}{{x(x-2)}^{2}}$•$\frac{{x}^{2}}{(x+2)(x-4)}$
=$\frac{1}{x-2}$,
当x=2-$\sqrt{2}$时,原式=$\frac{1}{2-\sqrt{2}-2}$=-$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
14.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
| A. | -3.5 | B. | +2.5  | C. | -0.6  | D. | +0.7  |
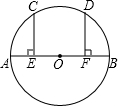 如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB,DF⊥AB,垂足分别为E、F,且AE=BF,$\widehat{AC}$与$\widehat{BD}$相等吗?为什么?
如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB,DF⊥AB,垂足分别为E、F,且AE=BF,$\widehat{AC}$与$\widehat{BD}$相等吗?为什么?