Question

13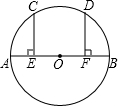．如图，AB是⊙O的直径，点C、D在⊙O上，CE⊥AB，DF⊥AB，垂足分别为E、F，且AE=BF，$\widehat{AC}$与$\widehat{BD}$相等吗？为什么？

Answer 1

分析 连接OC、OD，根据直角三角形全等的判定定理证明Rt△COE≌Rt△DOF，根据圆心角、弧、弦的关系证明结论．

解答 解：$\widehat{AC}$与$\widehat{BD}$相等，
证明：连接OC、OD，
∵AE=BF，OA=OB，
∴OE=OF，
在Rt△COE和Rt△DOF中，
$\left\{\begin{array}{l}{OE=OF}\\{OC=OD}\end{array}\right.$，
∴Rt△COE≌Rt△DOF，
∴∠AOC=∠BOD，
∴$\widehat{AC}$=$\widehat{BD}$．

点评 本题考查的是圆心角、弧、弦的关系和全等三角形的判定与性质，掌握在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等是解题的关键．