题目内容
8.某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A-非常喜欢”、“B-比较喜欢”、“C-不太喜欢”、“D-很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是比较喜欢;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
分析 (1)根据条形统计图与扇形统计图可以得到调查的学生数,从而可以的选B的学生数和选B和选D的学生所占的百分比,从而可以将统计图补充完整;
(2)根据(1)中补全的条形统计图可以得到众数;
(3)根据(1)中补全的扇形统计图可以得到该年级学生中对数学学习“不太喜欢”的人数.
解答  解:(1)由题意可得,
解:(1)由题意可得,
调查的学生有:30÷25%=120(人),
选B的学生有:120-18-30-6=66(人),
B所占的百分比是:66÷120×100%=55%,
D所占的百分比是:6÷120×100%=5%,
故补全的条形统计图与扇形统计图如右图所示,
(2)由(1)中补全的条形统计图可知,
所抽取学生对数学学习喜欢程度的众数是:比较喜欢,
故答案为:比较喜欢;
(3)由(1)中补全的扇形统计图可得,
该年级学生中对数学学习“不太喜欢”的有:960×25%=240(人),
即该年级学生中对数学学习“不太喜欢”的有240人.
点评 本题考查众数、用样本估计总体、扇形统计图、条形统计图,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | $\sqrt{45}-2\sqrt{5}=\sqrt{5}$ | B. | (π-3.14)0=0 | C. | a2•a5=a10 | D. | (a+b)2=a2+b2 |
3. 根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )
根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )
 根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )
根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{3}$ |
20.在下列运算中,计算正确的是( )
| A. | a2+a2=a4 | B. | a3•a2=a6 | C. | a6÷a2=a4 | D. | (a3)2=a5 |
17.式子$\frac{1}{1-x}$有意义,x的取值范围( )
| A. | x<1 | B. | x>1 | C. | x≠1 | D. | 全体实数 |
18.下列式子运算正确的是( )
| A. | a2+a3=a5 | B. | a8÷a2=a6 | C. | (a+1)0+($\frac{1}{2}$)-1=-1 | D. | $\sqrt{8}$$+\root{3}{-8}$=0 |
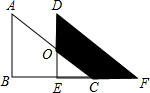 如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )
如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )


