题目内容
18.下列式子运算正确的是( )| A. | a2+a3=a5 | B. | a8÷a2=a6 | C. | (a+1)0+($\frac{1}{2}$)-1=-1 | D. | $\sqrt{8}$$+\root{3}{-8}$=0 |
分析 A:根据合并同类项的方法判断即可.
B:根据同底数幂的除法法则判断即可.
C:根据幂的乘方的运算方法判断即可.
D:根据算术平方根、立方根的性质和求法判断即可.
解答 解:∵a2+a3≠a5,
∴选项A不正确;
∵a8÷a2=a6,
∴选项B正确;
∵(a+1)0+($\frac{1}{2}$)-1=1+2=3,
∴选项C不正确;
∵$\sqrt{8}$+$\root{3}{-8}$=2$\sqrt{2}$-2≠0,
∴选项D不正确.
故选:B.
点评 (1)此题主要考查了同底数幂的除法法则:同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(4)此题还考查了立方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.
(5)此题还考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:①被开方数a是非负数;②算术平方根a本身是非负数.求一个非负数的算术平方根与求一个数的平方互为逆运算,在求一个非负数的算术平方根时,可以借助乘方运算来寻找.
(6)此题还考查了合并同类项的方法,要熟练掌握.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案 如图,将正方体的平面展开图重新折成正方体后,“数”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“数”字对面的字是( )| A. | 喜 | B. | 欢 | C. | 我 | D. | 学 |
| A. | 5,6 | B. | 5,5 | C. | 6,5 | D. | 6,6 |
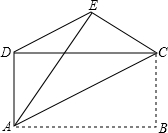 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则$\frac{AD}{AB}$的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则$\frac{AD}{AB}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
| A. | a3+a2=a5 | B. | a6÷a2=a3 | ||
| C. | (-3a2)•2a3=-6a6 | D. | (-ab-1)2=a2b2+2ab+1 |
| A. | x2+x2+x2 | B. | x2•x2•x2 | C. | 3x•3x | D. | 9x |
| A. |  | B. |  | C. |  | D. |  |

