题目内容
已知抛物线y=x2-(m+6)x+m+5.
(1)求证:无论m取什么实数,抛物线与x轴必有交点,且过x轴上一定点;
(2)当抛物线与x轴相交于A,B两不同点时,设其顶点为M,若△MAB是等腰直角三角形,求m的值.
(1)求证:无论m取什么实数,抛物线与x轴必有交点,且过x轴上一定点;
(2)当抛物线与x轴相交于A,B两不同点时,设其顶点为M,若△MAB是等腰直角三角形,求m的值.
考点:抛物线与x轴的交点
专题:
分析:(1)根据抛物线的表达式可化为交点式进而可求出抛物线和x轴有交点,解方程即可求出过x轴上一定点的坐标;
(2)由(1)可知A和B的坐标,把函数的表达式可化为顶点式进而可求出M点的坐标,因为△MAB是等腰直角三角形,所以MA=MB,进而可求出m的值.
(2)由(1)可知A和B的坐标,把函数的表达式可化为顶点式进而可求出M点的坐标,因为△MAB是等腰直角三角形,所以MA=MB,进而可求出m的值.
解答:(1)证明:∵y=x2-(m+6)x+m+5=(x-1)(x-m-5)=0
得到x1=1,x2=m+5,
∴无论m取什么实数,抛物线与x轴必有交点,且过x轴上一定点(1,0);
(2)解:A(1,0)B(m+5,0)(m+5≠1,即m≠-4)
y=[x-
(m+6)]2-
(m2+8m+16),
∴顶点M
((m+6),-
(m2+8m+16),
∵抛物线关于对称轴对称,
∴MA=MB,
∵△MAB是等腰直角三角形,
∴
(m+4)2+
(m+4)4=(m+4)2,
∴
+
(m+4)2=1,
∴m=-2或-6.
得到x1=1,x2=m+5,
∴无论m取什么实数,抛物线与x轴必有交点,且过x轴上一定点(1,0);
(2)解:A(1,0)B(m+5,0)(m+5≠1,即m≠-4)
y=[x-
| 1 |
| 2 |
| 1 |
| 4 |
∴顶点M
| 1 |
| 2 |
| 1 |
| 4 |
∵抛物线关于对称轴对称,
∴MA=MB,
∵△MAB是等腰直角三角形,
∴
| 1 |
| 2 |
| 1 |
| 8 |
∴
| 1 |
| 2 |
| 1 |
| 8 |
∴m=-2或-6.
点评:本题考查了抛物线于x轴交点的坐标,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
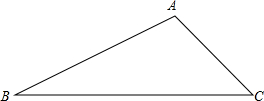 如图,在△ABC中,∠BAC是钝角,请画出AB边上的高CD,BC边上的中线AE,并将△ABC沿AE方向平移AE的长度.(请保留作图痕迹,并写出结论)
如图,在△ABC中,∠BAC是钝角,请画出AB边上的高CD,BC边上的中线AE,并将△ABC沿AE方向平移AE的长度.(请保留作图痕迹,并写出结论)