题目内容
已知y关于x的一次函数的图象过点(2,3),(-2,1),求当-2<y<2时,x的取值范围.
考点:待定系数法求一次函数解析式,一次函数的性质
专题:
分析:首先设y=kx+b,再把(2,3),(-2,1)代入可得关于k、b的方程组,再解方程组可得k、b的值,然后可得函数解析式,再根据-2<y<2可得关于x的不等式,再解即可.
解答:解:设y=kx+b,
∵图象过点(2,3),(-2,1),
∴
,
解得
,
∴y=
x+2,
∵-2<y<2,
∴-2<
x+2<2,
解得:-8<x<0.
∵图象过点(2,3),(-2,1),
∴
|
解得
|
∴y=
| 1 |
| 2 |
∵-2<y<2,
∴-2<
| 1 |
| 2 |
解得:-8<x<0.
点评:此题主要考查了待定系数法求一次函数解析式,以及函数与不等式,关键是正确求出一次函数解析式.

练习册系列答案
相关题目
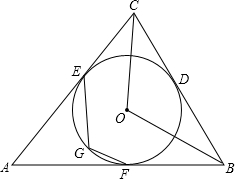 如图,圆O是△ABC的内切圆,D、E、F为切点,G为弧EF上的一点,请判断∠EGF与∠BOC是否相等,并说明理由.
如图,圆O是△ABC的内切圆,D、E、F为切点,G为弧EF上的一点,请判断∠EGF与∠BOC是否相等,并说明理由. 如图,△ABC绕点A旋转到AB′C′,BC与B′C′交于P,试说明AP平分∠BPC′.
如图,△ABC绕点A旋转到AB′C′,BC与B′C′交于P,试说明AP平分∠BPC′.