题目内容
两车从南北方向的路段AB的A端出发，分别向东、向西行进相同的距离，到达C、D两地．此时C、D到B的距离相等吗？请说明理由．
考点：全等三角形的应用
专题：
分析：作出图形，然后求出∠DAB=∠CAB=90°，AD=AC，再利用“边角边”证明△ABD和△ABC全等，根据全等三角形对应边相等可得BC=BD，从而得解．
解答：
解：C、D到B的距离相等．
理由如下：如图，由题意得，∠DAB=∠CAB=90°，AD=AC，
在△ABD和△ABC中，
，
∴△ABD≌△ABC（SAS），
∴BC=BD，
故C、D到B的距离相等．
解：C、D到B的距离相等．理由如下：如图，由题意得，∠DAB=∠CAB=90°，AD=AC，
在△ABD和△ABC中，
|
∴△ABD≌△ABC（SAS），
∴BC=BD，
故C、D到B的距离相等．
点评：本题考查了全等三角形的应用，读懂题目信息，判断出两全等三角形是解题的关键，作出图形更形象直观．
练习册系列答案
小学教材全测系列答案
相关题目
如图，在⊙O中，已知弦AB、CD互相垂直，连接AD、BC，作AD的弦心距OE，求证：CB=2EO．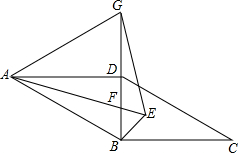
在?ABCD中，对角线BD⊥BC，G为BD延长线上一点且△ABG为等边三角形，∠BAD、∠CBD的平分线相交于点E，连接AE交BD于F，连接GE．
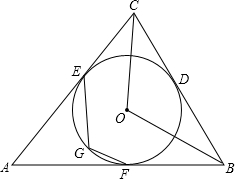如图，圆O是△ABC的内切圆，D、E、F为切点，G为弧EF上的一点，请判断∠EGF与∠BOC是否相等，并说明理由．