题目内容
已知y-3与4x-2成正比例,且当x=1时,y=5.
(1)求y与x的函数关系式;
(2)求当x=-2时的函数值;
(3)如果y的取值范围是0≤y≤5,求x的取值范围.
(1)求y与x的函数关系式;
(2)求当x=-2时的函数值;
(3)如果y的取值范围是0≤y≤5,求x的取值范围.
考点:待定系数法求一次函数解析式,一次函数的性质
专题:
分析:(1)首先设y-3=k(4x-2),再把x=1,y=5代入可得关于k的方程,再解出k的值可得答案;
(2)把x=-2代入函数解析式可得答案;
(3)根据y的取值范围,结合一次函数解析式,利用等量代换可得关于x的不等式组,再解不等式即可.
(2)把x=-2代入函数解析式可得答案;
(3)根据y的取值范围,结合一次函数解析式,利用等量代换可得关于x的不等式组,再解不等式即可.
解答:解:(1)设y-3=k(4x-2),
∵当x=1时,y=5,
∴5-3=k(4×1-2),
解得:k=1,
∴y与x的函数关系式为y-3=4x-2,
即y=4x+1;
(2)把x=-2代入y=4x+1可得:y=-7;
(3)∵0≤y≤5,
∴0≤4x+1≤5,
解得:-
≤x≤1.
∵当x=1时,y=5,
∴5-3=k(4×1-2),
解得:k=1,
∴y与x的函数关系式为y-3=4x-2,
即y=4x+1;
(2)把x=-2代入y=4x+1可得:y=-7;
(3)∵0≤y≤5,
∴0≤4x+1≤5,
解得:-
| 1 |
| 4 |
点评:此题主要考查了待定系数法求一次函数解析式,以及求函数值,关键掌握待定系数法求一次函数解析式一般步骤:
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;
(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;
(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;
(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;
(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )
如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )| A、90° | B、100° |
| C、110° | D、120° |
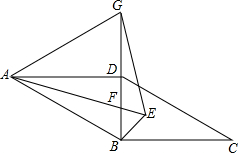 在?ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.
在?ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE. 如图,△ABC绕点A旋转到AB′C′,BC与B′C′交于P,试说明AP平分∠BPC′.
如图,△ABC绕点A旋转到AB′C′,BC与B′C′交于P,试说明AP平分∠BPC′.