题目内容
试求出所有这样的正整数a,使得关于x的二次方程ax2+2(2a-1)x+4a-3=0至少有一个整数根.
考点:一元二次方程的整数根与有理根,根的判别式
专题:
分析:首先利用根的判别式求出a的取值范围,然后得到正整数a的值,最后验证方程是否有整数根.
解答:解:∵关于x的二次方程ax2+2(2a-1)x+4a-3=0有实根,
∴
.
解得:
.
∵a是正整数,∴a=1.
当a=1时,原方程为x2+2x+1=0.
解得:x1=x2=-1.
∴满足要求的正整数a为1.
∴
|
解得:
|
∵a是正整数,∴a=1.
当a=1时,原方程为x2+2x+1=0.
解得:x1=x2=-1.
∴满足要求的正整数a为1.
点评:本题主要考查了根的判别式的应用,需要注意的是求出a的值后要检验方程是否有整数根.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )
如图,在矩形ABCD中,AC与BD交于点O,若AB=3,AC=6,则∠AOD等于( )| A、90° | B、100° |
| C、110° | D、120° |
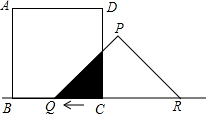 已知有一边为5cm的正方形ABCD和等腰三角形PQR,PQ=PR=5cm,QR=5
已知有一边为5cm的正方形ABCD和等腰三角形PQR,PQ=PR=5cm,QR=5