题目内容
8.在平面直角坐标系中,O为坐标原点,点A的坐标为(a,-a),点B坐标为(b,c),a、b、c满足$\left\{\begin{array}{l}{3a+2b+c=8}\\{a-b+2c=-4}\end{array}\right.$.(1)若a没有平方根,判断点A在第几象限并说明理由;
(2)若点A到y轴的距离是点B到y轴距离的3倍,求点B的坐标;
(3)点D的坐标为(2,-4),△OAB的面积是△DAB面积的2倍,求点B的坐标.
分析 (1)根据负数没有平方根进行解答即可;
(2)解方程组得出关于a的代数式,分两种情况解答即可;
(3)根据AB坐标判断线段AB平行于x轴,进而解答即可.
解答 解:(1)∵a没有平方根,
∴a<0,
∴-a>0,
∴点A(a,-a)在第二象限;
(2)由方程组$\left\{\begin{array}{l}{3a+2b+c=8}\\{a-b+2c=-4}\end{array}\right.$,用a表示b,c得b=-a+4,c=-a,
再利用点A到y轴的距离是点B到y轴距离的3倍得:
|-a|=3|-a+4|,
可以分两种情况分析:
①-a=3(-a+4),
解之,得a=6,所以b=-2,c=-6;
②-a=-3(-a+4),
解之,得a=3,所以b=1,c=-3;
综上,B(-2,-6)或B(1,-3);
(3)利用A(a,-a)和B(-a+4,-a),
可以判断线段AB平行于x轴.由点D的坐标(2,-4),
△OAB的面积是△DAB面积的2倍,
可以判断点A和点B在x轴的下方,则a>0,
$\frac{1}{2}$AB•a=2×$\frac{1}{2}$ AB•|a-4|,
解得,a=$\frac{8}{3}$或a=8,
所以,B($\frac{4}{3}$,$-\frac{8}{3}$)或B(-4,-8).
点评 本题考查了坐标与图形性质:利用点的坐标计算线段的长和判断线段与坐标轴的位置关系.也考查了三角形的面积公式.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
13.下列实数$\frac{π}{2}$,$\frac{22}{7}$,0.7171171117…(相邻的两个7之间1的个数逐次加1),$\root{3}{9}$,$\sqrt{\frac{1}{2}}$中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.Rt△的三边a、b、c,则关于x的方程a(x2-1)-2cx+b(x2+1)=0的根的情况为( )
| A. | 有两个相等的实根 | B. | 有实根 | ||
| C. | 有两个不相等的实根 | D. | 没有实根 |
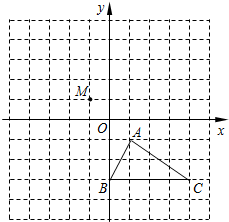 在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
 如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?
如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?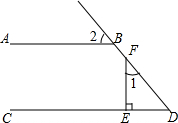 如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.
如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.