题目内容
3. 如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?
如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?
分析 由三角函数分别求出BC、CD,即可得出BD的长.
解答 解:由题意知:∠CAB=90°-30°=60°,△ABC是直角三角形,
在Rt△ABC中,tan60°=$\frac{BC}{AC}$,
∴BC=AC•tan60°=24$\sqrt{3}$米,
∵∠CAD=90°-60°=30°,
∴CD=AC1tan30°=24×$\frac{\sqrt{3}}{3}$=8$\sqrt{3}$(米),
∴BD=BC-CD=24$\sqrt{3}$-8$\sqrt{3}$=16$\sqrt{3}$(米);
答:荷塘宽BD为16$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用;由三角函数求出BC和CD是解决问题的关键解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.-27的立方根是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | ±9 |
16.不等式组$\left\{\begin{array}{l}{x-2<0}\\{2x+6>0}\end{array}\right.$的解集为( )
| A. | -2<x<3 | B. | -3<x<2 | C. | x<2 | D. | x>-3 |
11.估计$\sqrt{7}-2$的值在( )
| A. | 0到1之间 | B. | 1到2之间 | C. | 2到3之间 | D. | 3至4之间 |
15.$\sqrt{(-49)^{2}}$的平方根是( )
| A. | 49 | B. | 7 | C. | ±7 | D. | ±49 |
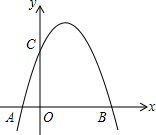 如图所示,在平面直角坐标系中,抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上.
如图所示,在平面直角坐标系中,抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上.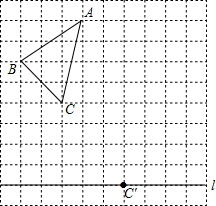 如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A′B′C′,点C的对应点是直线上的格点C′.
如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A′B′C′,点C的对应点是直线上的格点C′.