题目内容
20.Rt△的三边a、b、c,则关于x的方程a(x2-1)-2cx+b(x2+1)=0的根的情况为( )| A. | 有两个相等的实根 | B. | 有实根 | ||
| C. | 有两个不相等的实根 | D. | 没有实根 |
分析 判断根的情况就是判断判别式△与0的大小关系;a、b、c没有确定哪条是直角边,所以需要分类讨论,利用勾股定理化简根的判别式.
解答 解:化简原方程为:(a+b)x2-2cx+b-a=0,
∴△=4c2-4(b2-a2)=4(a2+c2-b2),
a、b、c都为正数;
当a为斜边时,a2=b2+c2,△=8c2>0,此时方程有两不等实根.
同理当b为斜边时,△=0,此时方程有两相等实根.
当c为斜边时,△=8a2>0,此时方程有两不等实根.
综上,故选B.
点评 本题主要考查了直角三角形三边关系、一元二次方程的根的判别式等知识点.重点是在直角三角形中,斜边未定,需要分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.估计$\sqrt{7}-2$的值在( )
| A. | 0到1之间 | B. | 1到2之间 | C. | 2到3之间 | D. | 3至4之间 |
15.$\sqrt{(-49)^{2}}$的平方根是( )
| A. | 49 | B. | 7 | C. | ±7 | D. | ±49 |
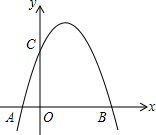 如图所示,在平面直角坐标系中,抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上.
如图所示,在平面直角坐标系中,抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上.