题目内容
3.在实数范围内分解下列因式(1)x2-5
(2)3x2-5
(3)x4-9.
分析 (1)原式利用平方差公式分解即可;
(2)原式变形后,利用平方差公式分解即可;
(3)原式利用平方差公式分解即可.
解答 解:(1)原式=(x+$\sqrt{5}$)(x-$\sqrt{5}$);
(2)原式=($\sqrt{3}$x+$\sqrt{5}$)($\sqrt{3}$x-$\sqrt{5}$);
(3)原式=(x2+3)(x2-3)=(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$).
点评 此题考查了实数范围内分解因式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
13.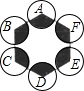 如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )
如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )
 如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )
如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )| A. | 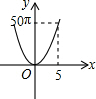 | B. | 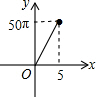 | C. | 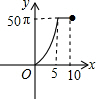 | D. | 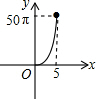 |
13.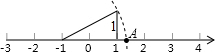 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )
 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )| A. | -$\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$+1 |
 如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.
如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.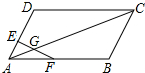 如图,点E为?ABCD的AD边上一点,且AE:ED=1:3,点F为AB的中点,EF交AC于点G,则AG:GC等于1:5.
如图,点E为?ABCD的AD边上一点,且AE:ED=1:3,点F为AB的中点,EF交AC于点G,则AG:GC等于1:5.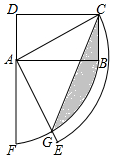 如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.
如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.