题目内容
11.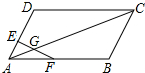 如图,点E为?ABCD的AD边上一点,且AE:ED=1:3,点F为AB的中点,EF交AC于点G,则AG:GC等于1:5.
如图,点E为?ABCD的AD边上一点,且AE:ED=1:3,点F为AB的中点,EF交AC于点G,则AG:GC等于1:5.
分析 设AC的中点为O,连接FO,又F是AB的中点,可得EO∥BC,EO=$\frac{1}{2}$BC,结合平行四边形的性质可证明△AEG∽△OFG,根据相似三角形的性质以及已知条件AE:ED=1:3,可求出AG:GC的值.
解答 解:设AC的中点为O,连接FO,又F是AB的中点,
∴FO∥BC,FO=$\frac{1}{2}$BC,
又AD∥BC,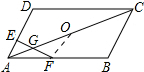
∴AE∥FO,
∴△AEG∽△OFG,
∴AG:GO=AE:FO,
∵AE:ED=1:3,AD=BC,
∴AE:BC=1:4,
∵OF:BC=1:2,
∴AE:OF=1:2,
∴AG:OG=1:2,
∵AO=$\frac{1}{2}$OC,
∴AG:CG=1:5,
故答案为:1:5.
点评 本题考查了平行四边形的性质,以及相似三角形的判定与性质,熟记平行四边形和相似三角形的各种性质是解题关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
20.下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④调查运动员兴奋剂的使用情况.其中适合采用抽样调查的是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
1.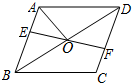 如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
 如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )| A. | 35° | B. | 55° | C. | 65° | D. | 75° |
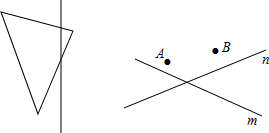 (1)以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.
(1)以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.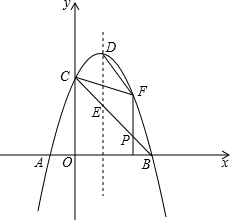 如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴相交于C点,顶点为D.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴相交于C点,顶点为D.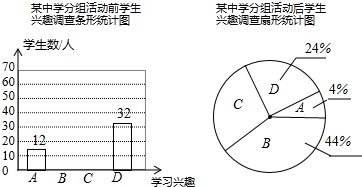
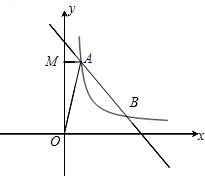 如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,