题目内容
8.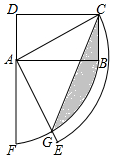 如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.
如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.
分析 根据勾股定理得到AC=2,由三角函数的定义得到∠CAB=30°,根据旋转的性质得到∠CAE=∠BAF=90°,求得∠BAG=60°,然后根据图形的面积即可得到结论.
解答 解:在矩形ABCD中,
∵AD=1,CD=$\sqrt{3}$,
∵AC=2,tan∠CAB=$\frac{BC}{AB}=\frac{AD}{CD}$=$\frac{\sqrt{3}}{3}$,
∴∠CAB=30°,
∵线段AC、AB分别绕点A顺时针旋转90°至AE、AF,
∴∠CAE=∠BAF=90°,
∴∠BAG=60°,
∵AG=AB=$\sqrt{3}$,
∴阴影部分面积=S△ABC+S扇形ABG-S△ACG=$\frac{1}{2}$×$\sqrt{3}$×1+$\frac{60•π×(\sqrt{3})^{2}}{360}$-$\frac{1}{2}$×$\sqrt{3}$×2=$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.
点评 本题考查了扇形的面积计算,矩形的性质,旋转的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
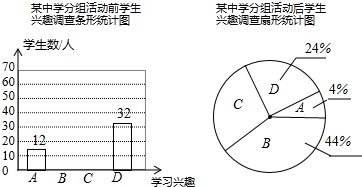
20.下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④调查运动员兴奋剂的使用情况.其中适合采用抽样调查的是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
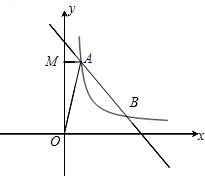 如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
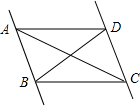 如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )