题目内容
12. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
分析 (1)延长AC交ON于点E,如图,利用互余计算出∠OCE=65°,再利用对顶角相等得到∠ACB=∠OCE=65°,再根据∠ACD=90°-∠ACB即可解决问题;
(2)接着在Rt△ABC中利用∠ACB的余弦可计算出BC,然后根据矩形的性质即可得到AD的长;
解答 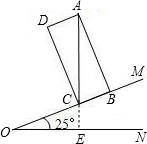 解:(1)延长AC交ON于点E,如图,
解:(1)延长AC交ON于点E,如图,
∵AC⊥ON,
∴∠OEC=90°,
在Rt△OEC中,
∵∠O=25°,
∴∠OCE=65°,
∴∠ACB=∠OCE=65°,
∴∠ACD=90°-∠ACB=25°
(2)∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,
在Rt△ABC中,∵cos∠ACB=$\frac{BC}{AC}$,
∴BC=AC•cos65°=5×0.42=2.1,
∴AD=BC=2.1.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.灵活应用勾股定理、互余关系和三角函数关系.

练习册系列答案
相关题目
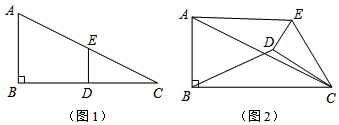
 如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)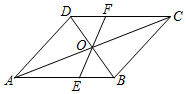 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F. 如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.求证:AE=BE.
如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.求证:AE=BE.