题目内容
2.某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同(Ⅰ)求甲、乙两种救灾物品每件的价格各是多少元?
(Ⅱ)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
分析 (1)设甲种救灾物品每件的价格是x元,则乙种救灾物品每件的价格是(x-10)元,根据数量=总价÷单价结合用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)根据总价=单价×数量列式计算,即可得出结论.
解答 解:(1)设甲种救灾物品每件的价格是x元,则乙种救灾物品每件的价格是(x-10)元,
根据题意得:$\frac{350}{x}$=$\frac{300}{x-10}$,
解得:x=70,
经检验,x=70是原分式方程的解,
∴x-10=60.
答:甲种救灾物品每件的价格是70元,则乙种救灾物品每件的价格是60元.
(2)70×$\frac{1}{1+3}$×2000+60×$\frac{3}{1+3}$×2000=125000(元).
答:若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金125000元.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据数量=总价÷单价.列出关于x的分式方程;(2)根据总价=单价×数量列式计算.

练习册系列答案
相关题目
11.有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和数量如下表所示,商家用加权平均数来确定什锦糖的单价.
(1)该什锦糖的单价为20元/千克.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中再加入甲、乙两种糖果共100千克,则最少需要加入甲种糖果多少千克?
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 15 | 20 | 25 |
| 千克(千克) | 30 | 40 | 30 |
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中再加入甲、乙两种糖果共100千克,则最少需要加入甲种糖果多少千克?
12.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.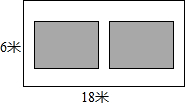 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为1米.
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为1米.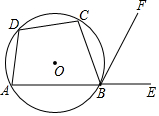 如图,四边形ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=100°,则∠FBE=50°.
如图,四边形ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=100°,则∠FBE=50°.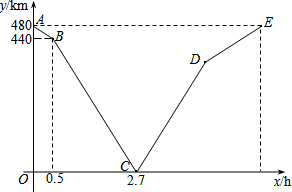 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设一辆车先出发xh后,另一辆车也开始行驶,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设一辆车先出发xh后,另一辆车也开始行驶,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题: