题目内容
7.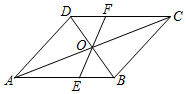 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
分析 (1)由四边形ABCD是平行四边形,可得OA=OC,AB∥CD,则可证得△AOE≌△COF(ASA),继而证得OE=OF;
(2)由△AOE≌△COF(ASA),可得EF=2OE=4,BE+CF=AB=6,继而求得答案.
解答 (1)证明:在□ABCD中,
∵AC与BD相交于点O,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,在△OAE和△OCF中,$\left\{\begin{array}{l}{∠OAE=∠OCF}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△OAE≌△OCF(ASA),
∴OE=OF.
(2)解:∵△OAE≌△OCF,
∴DF=AE,
∴BE+CF=AB=6,
又∵EF=2OE=4,
∴四边形BCFE的周长=BE+BE+CF+EF=6+4+5=15.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
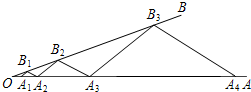 如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是32011.
如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是32011.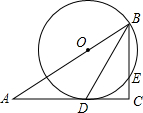 如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.