题目内容
10.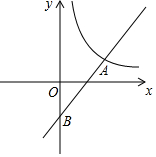 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(6,1),与y轴交于点B(0,-2)
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(6,1),与y轴交于点B(0,-2)(1)求a,b,k的值;
(2)请你在反比例函数y=$\frac{k}{x}$(x>0)的图象上找一点P,使得S△AOF=S△BOF,并写出点P的坐标.
分析 (1)根据A的坐标求出k的值,把A、B的坐标代入一次函数的解析式求出a、b;
(2)设P(m,$\frac{6}{m}$)且m>0,根据S△AOP=S△BOP得出$\frac{1}{2}$(1+$\frac{6}{m}$)×(6-m)=$\frac{1}{2}$×2•m,解得m的值即可求得.
解答 解:(1)依题意,k=6×1=6,
把A(6,1),B(0,-2)代入y=ax+b得$\left\{\begin{array}{l}{6a+b=1}\\{b=-2}\end{array}\right.$,
解得:a=$\frac{1}{2}$,b=-2;
(2)设P(m,$\frac{6}{m}$)且m>0,
∵S△AOP=S△BOP,
∴$\frac{1}{2}$(1+$\frac{6}{m}$)×(6-m)=$\frac{1}{2}$×2•m,
解得m=2$\sqrt{3}$,
∴P(2$\sqrt{3}$,$\sqrt{3}$).
点评 本题考查了一次函数和反比例函数的交点问题的应用以及三角形的面积,题目是一道比较典型的题目,难度适中.

练习册系列答案
相关题目
20.一辆汽车在公路上行驶,两次拐弯后,行驶的方向与原来的方向平行,则这两次拐弯的角度不可能是( )
| A. | 第一次向左拐40°,第二次向右拐40° | |
| B. | 第一次向右拐50°,第二次向左拐130° | |
| C. | 第一次向右拐60°,第二次向右拐120° | |
| D. | 第一次向左拐110°,第二次向右拐110° |
2.若$\sqrt{x-\frac{1}{8}}$+$\sqrt{\frac{1}{8}-x}$有意义,则$\root{3}{x}$=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{8}$ |
19. 如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )
如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )
 如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )
如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )| A. | ($\frac{1}{2}$)2017 | B. | ($\frac{1}{2}$)2016 | C. | ($\frac{1}{2}$)2015 | D. | ($\frac{1}{2}$)2014 |
 如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.
如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°. 己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.
己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.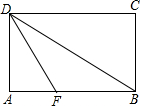 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°.
如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°.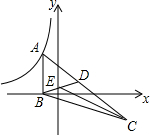 如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.
如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.