题目内容
19. 如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )
如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )| A. | ($\frac{1}{2}$)2017 | B. | ($\frac{1}{2}$)2016 | C. | ($\frac{1}{2}$)2015 | D. | ($\frac{1}{2}$)2014 |
分析 根据30°角所对的直角边等于斜边的一半得出O1A1=$\frac{1}{2}$OA1=$\frac{1}{2}$,O2A2=$\frac{1}{2}$O1A2=($\frac{1}{2}$)2,O3A3=$\frac{1}{2}$O2A3=($\frac{1}{2}$)3,即点A1的纵坐标为$\frac{1}{2}$;点A2的纵坐标为($\frac{1}{2}$)2,点A3的纵坐标为($\frac{1}{2}$)3,以此类推,从中得出规律,即可求出答案.
解答 解:∵三角形OAA1是等边三角形,
∴OA1=OA=1,∠AOA1=60°,
∴∠O1OA1=30°.
在直角△O1OA1中,∵∠OO1A1=90°,∠O1OA1=30°,
∴O1A1=$\frac{1}{2}$OA1=$\frac{1}{2}$,即点A1的纵坐标为$\frac{1}{2}$;
同理,O2A2=$\frac{1}{2}$O1A2=($\frac{1}{2}$)2,O3A3=$\frac{1}{2}$O2A3=($\frac{1}{2}$)3,
即点A2的纵坐标为($\frac{1}{2}$)2,
点A3的纵坐标为($\frac{1}{2}$)3,
…
∴点A2017的纵坐标为($\frac{1}{2}$)2017.
故选A.
点评 此题考查了规律型:点的坐标,等边三角形的性质,解答此题的关键是通过认真分析,根据30°角所对的直角边等于斜边的一半,从中发现规律.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
9.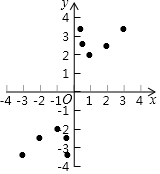 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是x≠0;
(2)如表是y与x的几组对应数值:
在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)进一步探究发现:该函数在第一象限内的最低点的坐标是(1,2),观察函数图象,写出该函数的另一条性质x>1时,y随x增大而增大;0<x<1时,y随x增大而减小;
(4)请你利用配方法证明:当x>0时,y=x+$\frac{1}{x}$的最小值为2.(提示:当x>0时x=($\sqrt{x}$)2,$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2)
 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:(1)自变量x的取值范围是x≠0;
(2)如表是y与x的几组对应数值:
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
(3)进一步探究发现:该函数在第一象限内的最低点的坐标是(1,2),观察函数图象,写出该函数的另一条性质x>1时,y随x增大而增大;0<x<1时,y随x增大而减小;
(4)请你利用配方法证明:当x>0时,y=x+$\frac{1}{x}$的最小值为2.(提示:当x>0时x=($\sqrt{x}$)2,$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2)
4. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
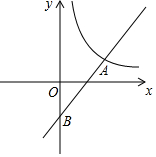 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(6,1),与y轴交于点B(0,-2)
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(6,1),与y轴交于点B(0,-2)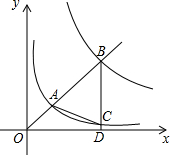 如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.
如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.