题目内容
20．一辆汽车在公路上行驶，两次拐弯后，行驶的方向与原来的方向平行，则这两次拐弯的角度不可能是（ ）| A． | 第一次向左拐40°，第二次向右拐40° | |
| B． | 第一次向右拐50°，第二次向左拐130° | |
| C． | 第一次向右拐60°，第二次向右拐120° | |
| D． | 第一次向左拐110°，第二次向右拐110° |
分析 依照题意画出图形，根据平行线的性质即可得出结论．
解答 解：∵两次转弯后仍在与原来方向平行的方向上行驶，
∴这两次拐弯的角度不可能是第一次向右拐50°，第二次向左拐130°，
故选B．
点评 本题考查了平行线的性质，解题的关键是根据行驶方向得出∠1=∠2．本题属于基础题，难度不大，解决该题型题目时，依照题意画出图形，利用数形结合解决问题是关键．
练习册系列答案
阅读快车系列答案
相关题目
11．下列各式中无论x为任何数都没有意义的是（ ）
| A． | $\sqrt{-7x}$ | B． | $\sqrt{-199{9x}^{3}}$ | C． | $\sqrt{{-0.1x}^{2}-1}$ | D． | $\root{3}{-{6x}^{2}-5}$ |
9．
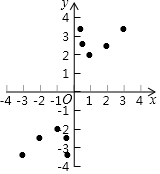某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究，探究过程如下，请补充完整：
（1）自变量x的取值范围是x≠0；
（2）如表是y与x的几组对应数值：
在平面直角坐标系中，描出了以表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）进一步探究发现：该函数在第一象限内的最低点的坐标是（1，2），观察函数图象，写出该函数的另一条性质x＞1时，y随x增大而增大；0＜x＜1时，y随x增大而减小；
（4）请你利用配方法证明：当x＞0时，y=x+$\frac{1}{x}$的最小值为2．（提示：当x＞0时x=（$\sqrt{x}$）2，$\frac{1}{x}$=（$\frac{1}{\sqrt{x}}$）2）
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究，探究过程如下，请补充完整：（1）自变量x的取值范围是x≠0；
（2）如表是y与x的几组对应数值：
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
（3）进一步探究发现：该函数在第一象限内的最低点的坐标是（1，2），观察函数图象，写出该函数的另一条性质x＞1时，y随x增大而增大；0＜x＜1时，y随x增大而减小；
（4）请你利用配方法证明：当x＞0时，y=x+$\frac{1}{x}$的最小值为2．（提示：当x＞0时x=（$\sqrt{x}$）2，$\frac{1}{x}$=（$\frac{1}{\sqrt{x}}$）2）
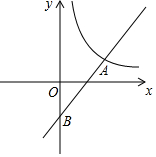如图，一次函数y=ax+b与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点A（6，1），与y轴交于点B（0，-2）