题目内容
12.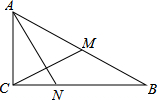 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由△ACN∽△BCA,得$\frac{CN}{AC}$=$\frac{AN}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$,根据三角函数定义即可解决问题.
解答  解:∵∠ACB=90°,
解:∵∠ACB=90°,
AM=BM,
∴CM=MB=MA=3,
∴∠B=∠MCB,
∵AN⊥CM,
∴∠CAN+∠ACM=90°,∠ACM+∠MCB=90°,
∴∠B=∠CAN,∴∠ACN=∠ACB=90°,
∴△ACN∽△BCA,
∴$\frac{CN}{AC}$=$\frac{AN}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$,
∴tan∠CAN=$\frac{CN}{AC}$=$\frac{2}{3}$.
故选A.
点评 本题考查相似三角形的判定和性质、锐角三角函数的定义、直角三角形斜边中线定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如下:
(Ⅰ)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组中抽取了6人.请将其余各组抽取的人数填入下表.
(Ⅱ)在(Ⅰ)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | 6 |
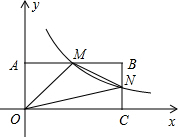 如图,在直角坐标系中,矩形OABC的顶点O是坐标原点,A,C分别在坐标轴上,点B的坐标为(4,2),M,N分别是AB,BC上的点,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O是坐标原点,A,C分别在坐标轴上,点B的坐标为(4,2),M,N分别是AB,BC上的点,反比例函数y=$\frac{k}{x}$的图象经过点M,N.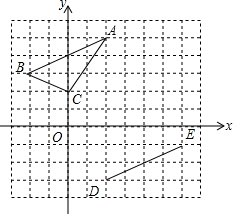 在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).
在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1). 将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.
将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.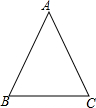 如图,等腰△ABC中,AB=AC.
如图,等腰△ABC中,AB=AC.