题目内容
4.已知关于x的一元二次方程x2-(m+6)x+3m+9=0的两个实数根分别为x1,x2.(1)求证:该一元二次方程总有两个实数根;
(2)若n=x1+x2-5,判断动点P(m,n)所形成的函数图象是否经过点A(4,5),并说明理由;
(3)若两根满足x1-2x2=m,求m的值.
分析 (1)由△=b2-4ac,套入数据得出△=m2≥0,由此得出结论;
(2)由根与系数的关系得出x1+x2=m+6,结合n=x1+x2-5,可得出n=m+1,再验证点A是否在函数n=m+1上即可;
(3)由根与系数的关系结合x1-2x2=m,得出关于x1、x2、m的三元一次方程组,解方程组即可得出结论.
解答 (1)证明:∵△=b2-4ac=(m+6)2-4(3m+9)=m2+12m+36-12m-36=m2≥0,
∴该一元二次方程总有两个实数根.
(2)解:动点P(m,n)所形成的函数图象经过点A(4,5),理由如下:
∵x1+x2=m+6,n=x1+x2-5,
∴n=m+1,
∵当m=4时,n=5,
∴动点P(m,n)所形成的函数图象经过点A(4,5).
(3)解:由已知得:$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=m+6}\\{{x}_{1}•{x}_{2}=3m+9}\\{{x}_{1}-2{x}_{2}=m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-1}\\{{x}_{1}=3}\\{{x}_{2}=2}\end{array}\right.$.
故若两根满足x1-2x2=m,m的值为-1.
点评 本题考查了根与系数的关系、根的判别式以及解三元一次方程组,解题的关键是:(1)找出b2-4ac≥0;(2)由两根之间的关系得出n=m+1;(3)结合根与系数的关系找出关于x1、x2、m的三元一次方程组.本题属于基础题,难度不大,解决该题型题目时,由根与系数的关系结合给定条件得出方程(或方程组)是关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.2015年,我市共接待参观旅游游客518 000人,这个数可用科学记数法表示为( )
| A. | 0.518×104 | B. | 5.18×105 | C. | 51.8×106 | D. | 518×103 |
15.在-3、0、4、0.5这四个数中最小的数是( )
| A. | -3 | B. | 0.5 | C. | 0 | D. | 4 |
12.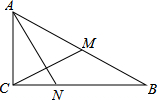 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
13.中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中12.6万用科学记数法表示应为( )
| A. | 1.26×106 | B. | 12.6×104 | C. | 1.26×105 | D. | 0.126×106 |
 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).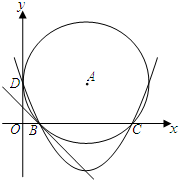 如图,在直角坐标系中,圆A与x轴交于点B、C,与y轴相切于点D,抛物线y=$\frac{1}{4}{x^2}-\frac{5}{2}$x+4经过B、C、D三点.
如图,在直角坐标系中,圆A与x轴交于点B、C,与y轴相切于点D,抛物线y=$\frac{1}{4}{x^2}-\frac{5}{2}$x+4经过B、C、D三点.