题目内容
17. 将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.
将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.
分析 当AC⊥AB时,重叠三角形面积最小,此时△ABC是等腰直角三角形,利用三角形面积公式即可求解.
解答 解:如图,当AC⊥AB时,三角形面积最小,
∵∠BAC=90°∠ACB=45°
∴AB=AC,
∴S△ABC=$\frac{1}{2}$×AC•BC=$\frac{1}{2}$AC2=4.5cm2.
故答案是:3.
点评 本题考查了折叠的性质,发现当AC⊥AB时,重叠三角形的面积最小是解决问题的关键.

练习册系列答案
相关题目
12.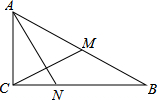 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
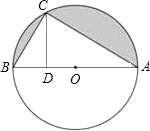 如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2.
如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2.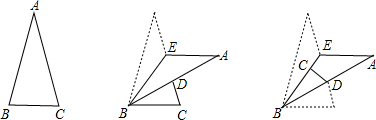
 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).